高中数学 第3章本章优化总结精品课件 新人教A版选修2-3 课件VIP免费

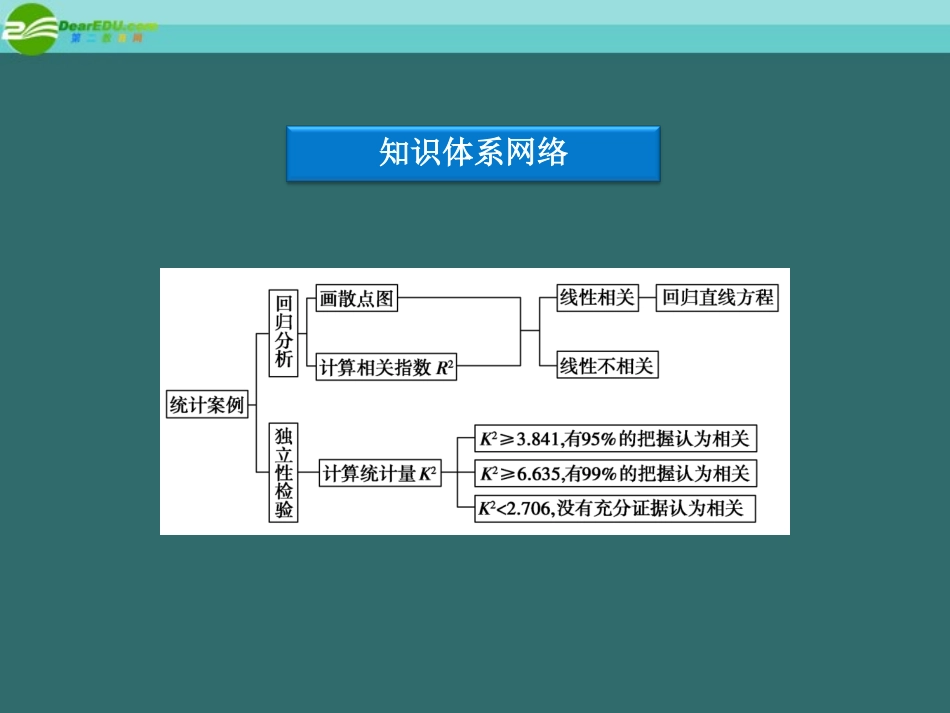
本章优化总结专题探究精讲知识体系网络本章优化总结知识体系网络专题探究精讲回归分析1．回归直线y^＝a^＋b^x中的斜率b^和截距a^是通过最小二乘法及回归直线过样本点中心(x，y)来确定的．2．残差分析，残差为e^i＝yi－y^i.3．相关指数R2＝1－i＝1nyi－y^i2i＝1nyi－y2，R2的值越大，说明残差平方和越小，也就是说模型的拟合效果越好．某商场经营一批进价是30元/台的小商品，在市场试验中发现，此商品的销售单价x(x取整数)元与日销售量y台之间有如下对应数据：例1单价x/元35404550日销量y/台56412811(1)画出散点图并说明y与x是否具有线性相关关系？如果有，求出线性回归方程；(方程的斜率保留一个有效数字)(2)设经营此商品的日销售利润为P元，根据(1)写出P关于x的函数关系式，并预测当销售单价x为多少元时，才能获得最大日销售利润？【解】(1)散点图如图所示：从图中可以看出这些点大致分布在一条直线附近，因此两个变量具有线性相关关系．设回归直线方程为y^＝b^x＋a^，由题意知x＝42.5，y＝34，则求得b^＝i＝14xi－xyi－yi＝14xi－x2＝－370125≈－3.a^＝y－b^x＝34－(－3)×42.5＝161.5.∴y^＝－3x＋161.5.(2)依题意有P＝(－3x＋161.5)(x－30)＝－3x2＋251.5x－4845＝－3(x－251.56)2＋251.5212－4845.∴当x＝251.56≈42时，P有最大值．即预测销售单价为42元时，能获得最大日销售利润．独立性检验独立性检验是对两个分类变量间是否存在相关关系的一种案例分析方法．常用的直观方法为画等高条形图．等高条形图由于是等高的，因此它能直观地反映两个分类变量之间的差异的大小，而利用假设的思想方法，计算出某一个随机变量K2的值来判断更精确些．为了解决高二年级统计案例入门难的问题，某校在高一年级的数学教学中着重加强统计思想的渗透，并设有对照班，下面是高二年级统计案例的测验成绩(单位：分)统计表的一部分，试分析实验效果.例270及70分以下70分以上总计对照班123850实验班321850总计4456100【解】根据列联表中的数据，由公式得：K2的观测值k＝nad－bc2a＋bc＋da＋cb＋d＝10032×38－18×12250×50×44×56≈16.234.因为16.234>10.828，所以，在犯错误的概率不超过0.001的前提下认为：高二统计案例的测试成绩与高一数学教学中增加统计思想的渗透有联系．本部分内容讲解结束点此进入课件目录点此进入课件目录按ESC键退出全屏播放按ESC键退出全屏播放谢谢使用