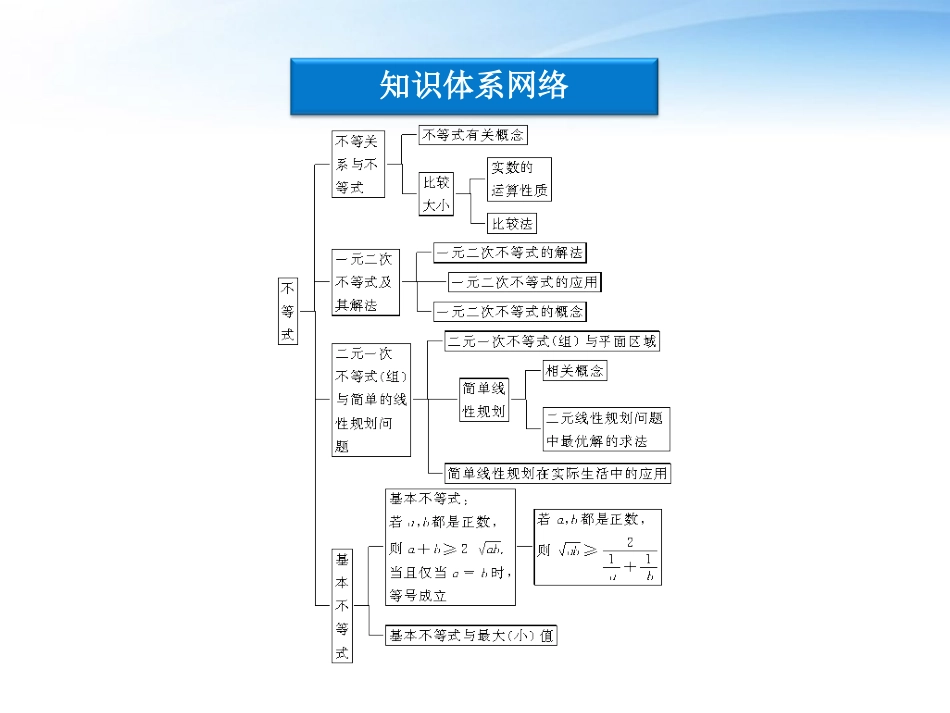
本章优化总结专题探究精讲本章优化总结知识体系网络知识体系网络专题探究精讲不等式的性质题型特点:利用不等式性质可以比较两个数(式)的大小,常常与函数、三角函数、数列、几何等知识结合运用.多以选择题、填空题的形式出现,题目难度不大.知识方法:不等式真假的判断,要依靠其适用范围和条件来确定,举反例是判断命题为假的一个好方法,用特例法验证时要注意,适合的不一定对,不适合的一定错,故特例只能否定选择项,只要四个中排除了三个,剩下的就是正确答案了.如果a,b,c满足c<b<a且ac<0,则以下列选项中不一定成立的是()A.ab>acB.c(b-a)>0C.cb2<ab2D.ac(a-c)<0例例11【解析】c<b<a,ac<0⇒a>0,c<0.【解析】c<b<a,ac<0⇒a>0,c<0.【答案】C一元二次不等式的解法题型特点:一元二次不等式主要考查它们的解法,求解时,往往结合一元二次方程的判别式、根的存在形式等.常与集合、函数、三角函数等知识综合考查.各种题型都可能出现,难度为中等.知识方法:解一元二次不等式时,一定要注意二次项系数对不等式解集的影响.解题时,首先将二次项系数化为正,在二次项系数为正的前提下,结合不等号的方向写出不等式的解集.口诀是:“大于在两边,小于取中间”.对于含有参数的不等式,由于参数的取值范围不同,其结果就不同,因此必须对参数进行分类讨论,即要产生一个划分参数的标准.解关于x的不等式:x2+(1-a)x-a<0.【解】方程x2+(1-a)x-a=0的解为x1=-1,x2=a.函数y=x2+(1-a)x-a的图象开口向上,所以(1)当a<-1时,原不等式解集为{x|a<x<-1};(2)当a=-1时,原不等式解集为;∅(3)当a>-1时,原不等式解集为{x|-1<x<a}.例例22线性规划问题题型特点:已知二元一次不等式(组)作出可行域,再求其面积,或者在约束条件下求目标函数的最值以及简单的实际问题,题型多以选择题出现,难度为中等题.知识方法:利用图解法解决线性规划问题的一般步骤如下:(1)作出可行域,即将线性约束条件中的每一个不等式所表示的平面区域作出,并求其公共部分.(2)作出目标函数的等值线.(3)确定最优解,即在可行域内平行移动目标函数等值线,从而确定最优解.(2010年高考福建卷)若x,y∈R且x≥1,x-2y+3≥0y≥x,则z=x+2y的最小值等于()A.2B.3C.5D.9例例33【解析】不等式组表示的平面区域为如图所示的阴影部分.当直线x+2y=z过点(1,1)时,目标函数z=x+2y取得最小值3,故选B.【答案】B(2010高考四川卷)某加工厂用某原料由甲车间加工出A产品,由乙车间加工出B产品.甲车间加工一箱原料需要耗费工时10小时可加工出7千克A产品,每千克A产品获利40元.乙车间加工一箱原料需耗工时6小时,可加工出4千克B产品,每千克B产品获利50元.甲、乙车间每天共能完成至多70箱原料的加工,每天甲、乙车间耗工时总和不得超过480小时,甲、乙两车间总获利最大的生产计划为()例例44A.甲车间加工原料10箱,乙车间加工原料60箱B.甲车间加工原料15箱,乙车间加工原料55箱C.甲车间加工原料18箱,乙车间加工原料50箱D.甲车间加工原料40箱,乙车间加工原料30箱【解析】设甲车间加工原料x箱,乙车间加工原料y箱,则x>0,x∈N,y>0,y∈N,x+y≤70,10x+6y≤480,甲乙两车间每天总获利为z=280x+200y,画出可行域,由线性规划知识可知当直线z=280x+200y经过x+y=70与10x+6y=480的交点(15,55)时,z=280x+200y取到最大值,因此,甲车间加工原料15箱,乙车间加工原料55箱,每天能够获得最大利润.【答案】B基本不等式的应用题型特点:基本不等式是高考必考内容,命题经常出现在选择题、填空题中.以考查基本不等式的应用为重点,兼顾考查代数式变形、化简能力等.大题一般不单独命题,但常与函数、实际问题相联系.知识方法:基本不等式通常用来求最值问题:一般用a+b≥2ab(a>0,b>0)解“定积求和,和最小”问题,用ab≤(a+b2)2解“定和求积,积最大”问题.一定要注意适用的范围和条件:“一正、二定、三相等”.特别是利用拆项、添项、配湊、分离变量等方法构造相定值条件对等号能否成立的验证.若等号不能取到,...