高三数学 立体几何中的向量方法(二)复习课件VIP免费

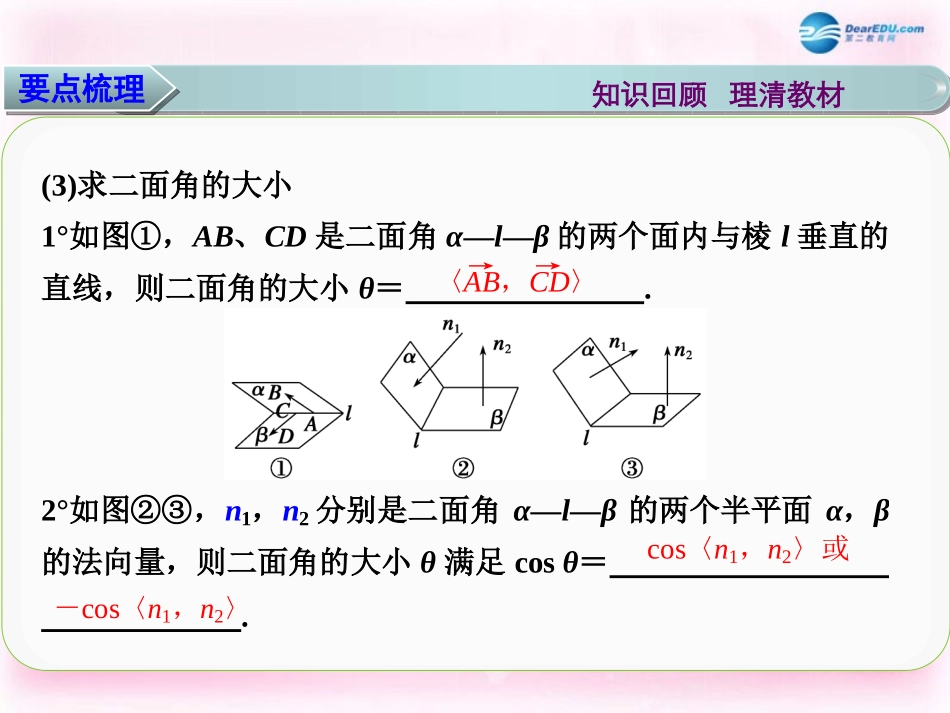
第八章立体几何§8.7§8.7立体几何中的向量方法立体几何中的向量方法（二）（二）————求空间角和距离求空间角和距离知识回顾理清教材要点梳理1.空间向量与空间角的关系(1)设异面直线l1，l2的方向向量分别为m1，m2，则l1与l2所成的角θ满足cosθ＝.(2)设直线l的方向向量和平面α的法向量分别为m，n，则直线l与平面α所成角θ满足sinθ＝.|cos〈m1，m2〉||cos〈m，n〉|知识回顾理清教材要点梳理(3)求二面角的大小1°如图①，AB、CD是二面角α—l—β的两个面内与棱l垂直的直线，则二面角的大小θ＝.2°如图②③，n1，n2分别是二面角α—l—β的两个半平面α，β的法向量，则二面角的大小θ满足cosθ＝.〈AB→，CD→〉cos〈n1，n2〉或－cos〈n1，n2〉知识回顾理清教材要点梳理2.点面距的求法如图，设AB为平面α的一条斜线段，n为平面α的法向量，则B到平面α的距离d＝.|AB→·n||n|题号答案12345BB41133(1)×夯实基础突破疑难夯基释疑90°(2)×(3)×(4)√(5)√(6)×【例1】长方体ABCD－A1B1C1D1中，AB＝AA1＝2，AD＝1，E为CC1的中点，则异面直线BC1与AE所成角的余弦值为()A.1010B.3010C.21510D.31010题型一求异面直线所成的角思维启迪解析答案思维升华【例1】长方体ABCD－A1B1C1D1中，AB＝AA1＝2，AD＝1，E为CC1的中点，则异面直线BC1与AE所成角的余弦值为()A.1010B.3010C.21510D.31010本题可以通过建立空间直角坐标系，利用向量BC1→、AE→所成的角来求.题型一求异面直线所成的角思维启迪解析答案思维升华【例1】长方体ABCD－A1B1C1D1中，AB＝AA1＝2，AD＝1，E为CC1的中点，则异面直线BC1与AE所成角的余弦值为()A.1010B.3010C.21510D.31010建立坐标系如图，则A(1,0,0)，E(0,2,1)，B(1,2,0)，C1(0,2,2).BC1→＝(－1,0,2)，AE→＝(－1,2,1)，cos〈BC1→，AE→〉＝BC1→·AE→|BC1→|·|AE→|＝3010.所以异面直线BC1与AE所成角的余弦值为3010.题型一求异面直线所成的角思维启迪解析答案思维升华【例1】长方体ABCD－A1B1C1D1中，AB＝AA1＝2，AD＝1，E为CC1的中点，则异面直线BC1与AE所成角的余弦值为()A.1010B.3010C.21510D.31010题型一求异面直线所成的角建立坐标系如图，则A(1,0,0)，E(0,2,1)，B(1,2,0)，C1(0,2,2).BC1→＝(－1,0,2)，AE→＝(－1,2,1)，cos〈BC1→，AE→〉＝BC1→·AE→|BC1→|·|AE→|＝3010.所以异面直线BC1与AE所成角的余弦值为3010.B思维启迪解析答案思维升华【例1】长方体ABCD－A1B1C1D1中，AB＝AA1＝2，AD＝1，E为CC1的中点，则异面直线BC1与AE所成角的余弦值为()A.1010B.3010C.21510D.31010B用向量方法求两条异面直线所成的角，是通过两条直线的方向向量的夹角来求解，而两异面直线所成角的范围是θ∈0，π2，两向量的夹角α的范围是[0，π]，所以要注意二者的区别与联系，应有cosθ＝|cosα|.题型一求异面直线所成的角思维启迪解析答案思维升华跟踪训练1已知直四棱柱ABCD－A1B1C1D1中，底面ABCD为正方形，AA1＝2AB，E为AA1的中点，则异面直线BE与CD1所成角的余弦值为()A.1010B.15C.31010D.35解析如图，以D为坐标原点建立如图所示空间直角坐标系.设AA1＝2AB＝2，则B(1,1,0)，E(1,0,1)，C(0,1,0)，D1(0,0,2)，∴BE→＝(0，－1,1)，CD1→＝(0，－1,2)，∴cos〈BE→，CD1→〉＝1＋22·5＝31010.C题型二求直线与平面所成的角【例2】如图，已知四棱锥P—ABCD的底面为等腰梯形，AB∥CD，AC⊥BD，垂足为H，PH是四棱锥的高，E为AD的中点.(1)证明：PE⊥BC；(2)若∠APB＝∠ADB＝60°，求直线PA与平面PEH所成角的正弦值.思维启迪思维升华解析【例2】如图，已知四棱锥P—ABCD的底面为等腰梯形，AB∥CD，AC⊥BD，垂足为H，PH是四棱锥的高，E为AD的中点.(1)证明：PE⊥BC；(2)若∠APB＝∠ADB＝60°，求直线PA与平面PEH所成角的正弦值.平面的法向量是利用向量方法解决位置关系或夹角的关键，本题可通过建立坐标系，利用待定系数法求出平面PEH的法向量.题型二求直线与平面所成的角思维启迪思维升华解析【例2】如图，已知四棱锥P—ABCD的底面为等腰梯形，AB∥CD，AC⊥BD，垂足为H，PH是四棱锥的高，E为AD的中点.(1)证明：PE⊥BC；(2)若∠APB＝∠ADB＝60°，求直线...