简易概率 高二数学概率知识的课件集合 人教版 高二数学概率知识的课件集合 人教版VIP免费

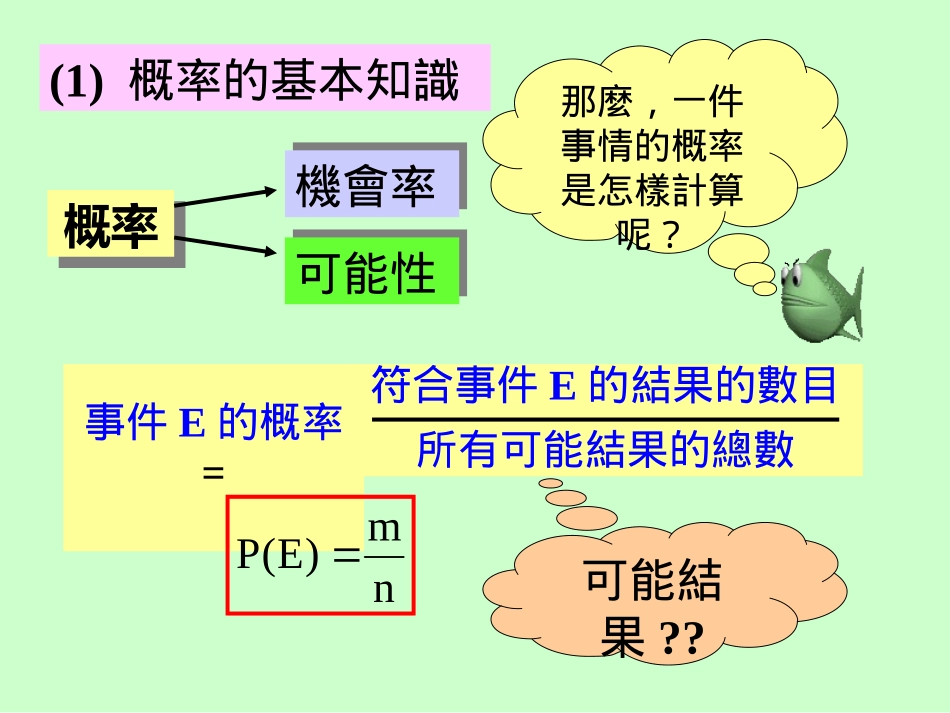
第七章簡易概率請按以下其中一個章節簡單概率的基本知識實驗概率較複雜的概率問題結束(1)概率的基本知識概率概率機會率機會率可能性可能性那麼，一件事情的概率是怎樣計算呢？符合事件E的結果的數目所有可能結果的總數事件E的概率=nm)E(P可能結果??例1:擲一枚均勻(均稱)的骰子，求擲出偶數的概率。可能的結果：{1，2，3，4，5，6}符合事件E(偶數)的結果：{2，4，6}nm)E(P可能結果的總數n=6符合事件E的結果的數目m=363)(P偶數2163)3(P點數32(a)大於3例2:擲一枚均勻(均稱)的骰子，求擲出下列點數的概率。62)2(P點數31(b)不大於2，，，0)1(P點數(c)小於1166)1(P點數(d)不小於11)E(P0結論:P(不可能事件)P(必然事件)例3:一袋中有紅球2個，藍球3個，白球5個，現從袋中隨意抽出一球，求下列事件發生的概率。(a)抽得紅球或白球(c)抽得的球並非白球(b)抽得黑球1052)(P紅球或白球107球的總數=2+3+5=10個P(黑球)=0P(並非白球)=P(紅球或藍球)103210521例4:從一副52張樸克牌中隨意抽出一張，求下列事件的概率是多少?一副樸克牌中有4種花色:黑色的黑桃(葵扇)和梅花、紅色的紅心和方塊(鑽石)，每種花色有13張牌。(a)抽得A(c)抽得紅心A(b)抽得梅花牌(d)抽得紅心牌或A例4:從一副52張樸克牌中隨意抽出一張，求下列事件的概率是多少?(a)P(A)=(a)抽得A(c)抽得紅心A(b)抽得梅花牌(d)抽得紅心牌或A524131(b)P(梅花)=521341(c)P(紅心A)=521(b)P(紅心牌或A)=5214135216134例5:從STTERESA中隨意抽出一個英文字母,求(a)抽出一個元音字母的概率(b)抽出一個輔音字母的概率(c)抽出'TIME'中的任何一字母的概率元音字母:A,E,I,O,U其餘為輔音字母STTERESA中共有8個字母(a)P(元音)=83(b)P(輔音)=85(c)該概率=8421STTERESASTTERESASTTERESA(2)實驗概率擲一枚均勻(均稱)的骰子，擲出'1'的概率610.167現在做一實驗，擲一枚均勻(均稱)的骰子多次，其結果如下:此為理論概率此為實驗概率擲出'1'的概率點數123456次數1881310746018=0.3擲骰總次數=18+8+13+10+7+4=60實驗概率—由實驗的結果計算出來的概率事件E發生的次數試驗的總次數事件E的實驗概率=實驗的次數越多，實驗概率理論概率擲骰實驗擲骰實驗例6:試利用軟件投擲兩枚骰子500次,並將結果列出。總點數23456789101112次數1528404962906864412914求下列事件的實驗概率(a)總點數小於4(b)總點數大於5但小於9擲骰實驗擲骰實驗(a)P(總點數小於4)=500(b)P(總點數大於5但小於9)=15+2850043086.050062+90+6844.0點數123456次數151817x1916若實驗的總次數為100次,求擲出4的實驗概率。15+18+17+x+19+16=100例7:以下是一個實驗的結果:x=15P(4)1001515.0例1:如果投擲兩枚硬幣，問得到下列結果的概率是多少？(a)2次正面(「公」)。(b)2次反面(「字」)。(c)1次正面和1次反面。較複雜的概率問題設H代表正面，T代表反面。可能的結果是HH、HT、TH、TT。可能的結果的數目=4(a)P(2次正面)41(c)P(1次正面和1次反面)42(b)P(2次反面)4121例2:一個家庭有3個孩子。求下列事件的概率:(a)這個家庭有3個男孩。(b)這個家庭有2個男孩和1個女孩。(c)這個家庭至少有1個男孩。設B代表男孩，G代表女孩。可能的結果是可能的結果的數目=8(a)P(BBB)81(c)P(至少有1個男孩)(b)P(2B1G)83811=1-P(沒有男孩)87BBBBBGBGBBGGGBBGBGGGBGGG例3:如果投擲三枚硬幣，求下列事件的概率:(a)3次正面。(b)2次反面及1次正面。(c)至少有1次反面。設H代表正面，T代表反面。可能的結果是可能的結果的數目=8(a)P(HHH)81(c)P(至少有1次反面)(b)P(2T1H)83811=1-P(沒有反面)87HHHHHTHTHHTTTHHTHTTTHTTT例4:投擲兩枚骰子，求擲得下列結果的概率:(a)點數的和是5。(b)點數的積是6。(c)點數的和是6或12。(d)至少有一枚骰子是5點。(e)點數的和最小是10。(f)點數的和小於5。可能的結果是可能的結果的數目=36(a)P(和是5)(c)P(和是6或12)(b)P(積是6)3636361234561(1,1)(1,2)(1,3)(1,4)(1,5)(1,6)2(2,1)(2,2)(2,3)(2,4)(2,5)(2,6)3(3,1)(3,2)(3,3)(3,4)(3,5)(3,6)4(4,1)(4,2)(4,3)(4,4)(4,5)(4,6)5(5,1)(5,2)(5,3)(5,...