高中数学 第二章 数列 复习课件 新人教A版必修5 课件VIP免费

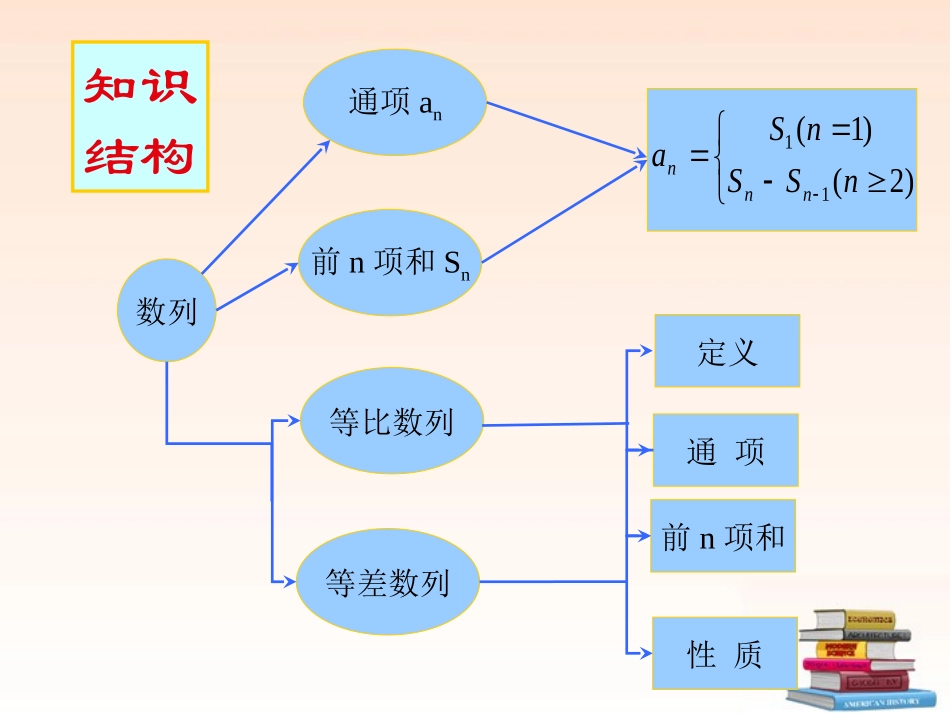
数列综合复习课高二数学必修（5）数列通项an等差数列前n项和Sn等比数列定义通项前n项和性质)2()1(11nSSnSannn知识结构等差数列等比数列定义通项公式中项公式前n项和公式an+1-an=d(常数),nN∈*an+1/an=q(常数),nN∈*an=a1+(n-1)dan=a1qn-1(a1,q≠0)若a，A，b成等差数列，则A=(a+b)/2.等差、等比数列的有关概念和公式若a，G，b成等比数列，则G2=ab（a,b≠0）11()2(1)2nnnaaSnnnad111(1)(1)(1)11nnnnaqSaaqaqqqq判断（或证明）数列为等差(等比）的方法：方法一（定义）(an+1－an=d或an－an－1=d(n≥2)方法二(等差中项)an+1+an－1=2an(n≥2)1、等差数列：11()(1)22nnnaannSnad2、等比数列：111(1)(1)(1)11nnnnaqSaaqaqqqq等差数列与等比数列前n项和注意公式的变形应用如：等差数列的前n项和公式：2)(2)(2)(1121mnmnnnaanaanaanSbnanndanddnnnaSn2121)2(22)1(等比数列的前n项和公式：qqaaqqaaqqaaqqaSmnmnnnn1111)1(1121111)1(q（1）nmaanmd（2）若2mnpqk则2mnpqkaaaaanmaadnmdkd2（3）若数列是等差数列，则也是等差数列}{na,,,,34232kkkkkkkSSSSSSS（4）{an}等差数列，其项数成等差数列，则相应的项构成等差数列等差数列的重要性质等差数列的重要性质5)对于等差数列{na}：若项数为n2则ndSS奇偶若项数为12n则naSS偶奇（中间项）1SnSn奇偶（2）2,mnpqk若mnpqaaaa则（1）nmnmaaqmnmnaaqq求（3）若数列是等比数列，则也是等比数列}{na,,,,34232kkkkkkkSSSSSSSkqq（4）{an}等比数列，若其项数成等差数列，则相应的项构成等比数列等比数列的重要性质等比数列的重要性质2SnqS偶奇5)在等比数列中，若项数为，则练习:•⒈在等差数列{an}中，a2=-2,a5=54，求a8=_____.•⒉在等差数列{an}中，若a3+a4+a5+a6+a7=450，则a2+a8的值为_________.•⒊在等差数列{an}中，a15=10,a45=90,则a60=__________.••⒋在等差数列{an}中，a1+a2=30,a3+a4=120,则a5+a6=_____.110运用性质：an=am+(n-m)d或等差中项运用性质：若n+m=p+q则am+an=ap+aq运用性质：从原数列中取出偶数项组成的新数列公差为2d.(可推广)运用性质：若{an}是公差为d的等差数列{cn}是公差为d′的等差数列，则数列{an+cn}是公差为d+d′的等差数列。180130210kk练习:•⒈在等比数列{an}中，a2=-2,a5=54，a8=.•⒉在等比数列{an}中，且an＞0，a2a4+2a3a5+a4a6=36,那么a3+a5=_.•⒊在等比数列{an}中，a15=10,a45=90,则a60=__________.•⒋在等比数列{an}中，a1+a2=30,a3+a4=120,则a5+a6=_____.-14586270480或-270练习：两个等差数列{na}、{nb}的前n项之和分别为,,/nnSS且7253/nnSSnn，则_______1515ba。解:2)(,2)(1/1nnnnbbnSaanS∴nnbbaa117253nn令,29n则有：6582291291bbaa而1515291291babbaa∴1515ba6582常见的求和公式123(1)2nnSnn22221123(1)(21)6nSnnnn333321123[(1)]2nSnnn专题一：一般数列求和法专题一：一般数列求和法①倒序相加法求和，如an=3n+1②错项相减法求和，如an=(2n-1)2n③分组法求和，如an=2n+3n④裂项相加法求和，如an=1/n(n+1)⑤公式法求和，如an=2n2-5n专题一：一般数列求和法专题一：一般数列求和法一、倒序相加法解：例1:()(1)1,1231999()()()...().2000200020002000fxfxffff已知求的值12100019981999()()()()()2000200020002000200019991998100021()()()()()200020002000200020001199921998()()()()200020002000200019991()(2000200SfffffSfffffSSffffff)01199919992S二、错位相减法23,3,5(21)(0)naaanaan例2、求数列，的前项和2335(21)nnSaaana①解：1,a当时132)12()...(2)1(...