高中数学 3.3.2两点间的距离课件 新人教A版必修2VIP免费

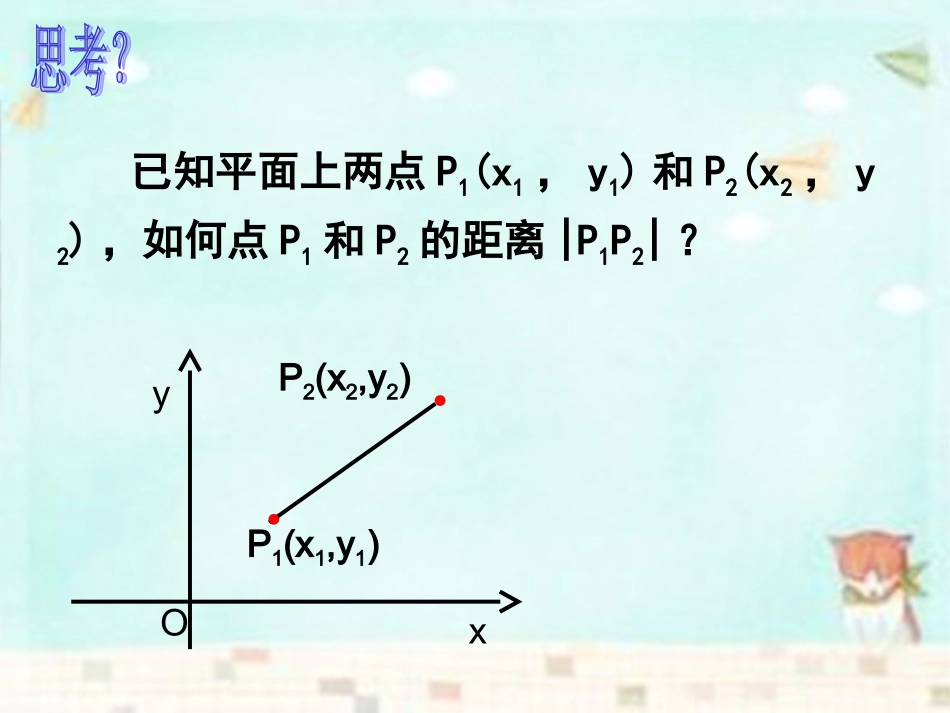
3.3.2两点间的距离目标：1.理解并掌握平面上两点之间的距离公式及推导方法2.能熟练应用距离公式解决问题，进一步体会用代数方法解决几何问题的思想已知平面上两点P1(x1，y1)和P2(x2，y2)，如何点P1和P2的距离|P1P2|？xyP1(x1,y1)P2(x2,y2)O思考：求两点A（0，2），B（0，-2）间的距离112233-1-1-2-2yxAB||||1221yyPPx1=x2,y1≠y2思考：求两点A（—2，0），B（3，0）间的距离112233-1-1-2-2yxAB||||1221xxPPx1≠x2,y1=y2思考：若将A移动到A’（—2，2）处，B（3，0）不变，求A’B间的距离。112233-1-1-2-2yxABA’思考：若再将B移动到B’（3，－2）处，A’（－2，2）不动，求A’B’间的距离。112233-1-1-2-2yxB’BA’C两点间距离公式推导xyP1(x1,y1)P2(x2,y2)Q(x2,y1)O221||||PQyy121||||PQxxx2y2x1y1xoy21yxQ，111yxP，222yxP，试求：两点间的距离已知：和，111yxP，222yxP，22121212()()PPxxyy当y1=y2时，1221||PPxx当x1=x2时，1221||PPyy两点间距离公式22122121||()()PPxxyy22||OPxy特别地，点P（x，y）到原点（0，0）的距离为一般地，已知平面上两点P1(x1，)和P2(x2，y2)，利用上述方法求点P1和P2的距离为1y练习（课本练习（课本106106页）页）1、求下列两点间的距离：(1)、A(6，0),B(-2，0)(2)、C(0，-4),D(0，-1)(3)、P(6，0),Q(0，-2)(4)、M(2，1),N(5，-1)解：（1）22AB=-2-6+0-0=8（2）22CD=0-0+-1+4=3（3）22PQ=0-6+-2-0=210（4）22521113MN练习练习22（课本（课本106106页）页）.|||,|||,),7,2(),2,1(:2的值并求得使轴上求一点在已知点例PAPBPAPxBA解：设所求点为P(x,0)，于是有114xx)7(02)(x|PB|52xx2)(01)(x|PA|222222114xx52xx得|PB||PA|由22解得x=1，所以所求点P(1,0)22222)(01)(1|PA|2、求在x轴上与点A(5,12)的距离为13的坐标；练习练习3、已知点P的横坐标是7，点P与点N(-1,5)间的距离等于10，求点P的纵坐标。yxo(b,c)(a+b,c)(a,0)(0,0)解：如图，以顶点A为坐标原点，AB所在直线为x轴，建立直角坐标系，则有A(0,0)。设B(a,0),D(b,c),由平行四边形的性质可得C(a+b,c)ABDC点C的纵坐标等于点D的纵坐标C、D两点横坐标之差为a例3:证明平行四边形四条边的平方和等于两条对角线的平方和。2222a|CD|,a|AB|222222cb|BC|,cb|AD|222222ca)-(b|BD|,cb)(a|AC|222222|BD||AC||BC||AD||CD||AB|因此，平行四边形四条边的平方和等于两条对角线的平方和。yxo(b,c)(a+b,c)(a,0)(0,0)ABDC第一步：建立坐标系，用坐标表示有关的量；第二步：进行有关的代数运算；第三步：把代数运算结果“翻译”所几何关系.练习已知△ABC是直角三角形，斜边BC的中点为M，建立适当的平面直角坐标系，证明：|AM|＝12|BC|.解以Rt△ABC的直角边AB，AC所在直线为坐标轴，建立如图所示的平面直角坐标系．设B，C两点的坐标分别为(b,0)，(0，c)．因为斜边BC的中点为M，所以点M的坐标为，即.)20,20(cb)2,2(cb由两点间距离公式得，|BC|＝0－b2＋c－02＝b2＋c2，|AM|＝0－b22＋0－c22＝12b2＋c2，所以|AM|＝12|BC|.例4设直线2x-y+1=0与抛物线相交于A、B两点，求|AB|的值.234yxx典例讲评8．x轴上任一点到定点(0,2)、(1,1)距离之和的最小值是()．A.B．2＋C.D.＋1解析作点(1,1)关于x轴的对称点(1，－1)，则距离之和最小值为.答案C2210510)21(12210．若动点P的坐标为(x,1－x)，x∈R，则动点P到原点的最小值是________．解析由距离公式得==，∴最小值为＝.答案22)1(xx1222xx21)21(22x212222例2.求下面函数的最小值5巩固训练P110页8题导练设计P139页1-11题120822xxxy