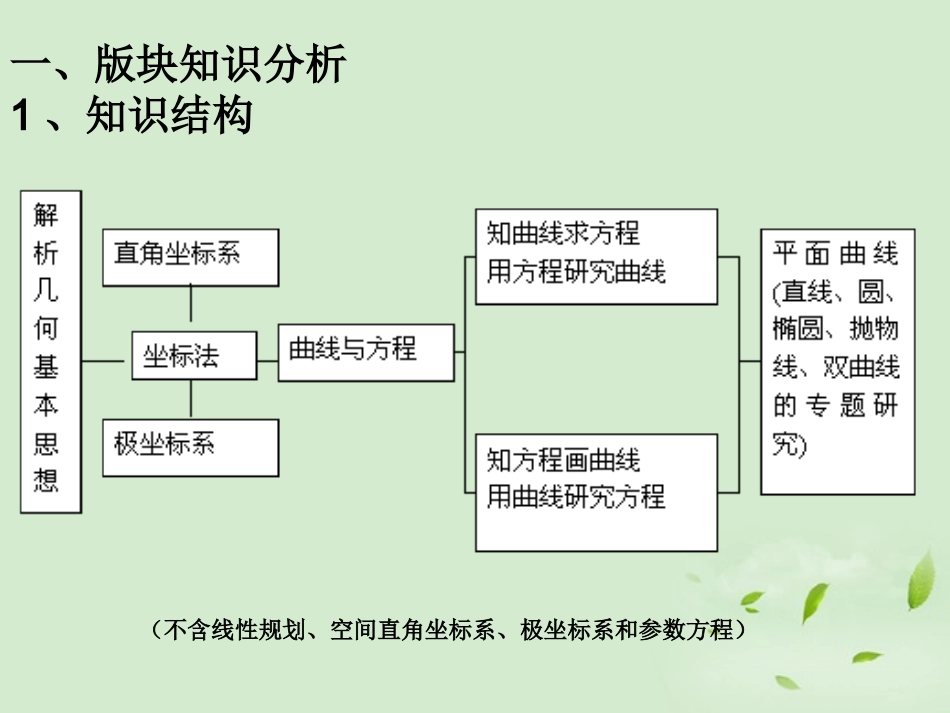
基于“减负增效”的解析几何复习教学建议基于“减负增效”的解析几何复习教学建议一、版块知识分析二、考纲考情分析三、亮点试题赏析四、“减负增效”略策一、版块知识分析1、知识结构(不含线性规划、空间直角坐标系、极坐标系和参数方程)一、版块知识分析1、知识结构一、版块知识分析1、知识结构一、版块知识分析2、内容本质在2004年高考上海理科卷中有这样一个试题:教材中“坐标平面上的直线”与“圆锥曲线”两章内容体现出解析几何的本质是__________.百度百科名片:解析几何系指借助坐标系,用代数方法研究几何对象之间的关系和性质的一门几何学分支,亦叫做坐标几何.基本介绍:解析几何包括平面解析几何和立体解析几何两部分.平面解析几何通过平面直角坐标系,建立点与实数对之间的一一对应关系,以及曲线与方程之间的一一对应关系,运用代数方法研究几何问题,或用几何方法研究代数问题.以上的解释指出了解析几何的主要工具是“坐标系”,研究的主要对象是“几何对象之间的关系和性质”,蕴含的主要核心数学思想是“数形结合思想”,他是沟通代数与几何的桥梁.回到2004年高考上海理科卷的试题,当时给出的参考答案是:用代数的方法研究图形的几何性质.(2004年高考上海理科卷)教材中“坐标平面上直线”与“圆锥曲线”两章内容体现出解析几何的本质是_____.这是一个问的很直接、很深刻的问题.不少学生也许能够解答一些解析几何的试题,但不一定能真正地感受到解析几何的本质是“用代数的方法研究图形的几何性质”.感受解析几何的本质,并通过实践有所领悟,对于形成正确的、良好的数学思维是有很大的帮助的.一、版块知识分析3、能力要求考试大纲中“考核目标与要求”所要求的五大能力两大意识,在高中解析几何课程中基本上都能找到良好的考查载体,其中重点考查的是抽象概括能力、推理论证能力、运算求解能力以及应用意识和创新意识.例1(2011年高考湖北卷理)如图,直角坐标系xOy所在平面为,直角坐标系''xOy(其中'y与y轴重合)所在的平面为,'45xOx.(Ⅰ)已知平面内有一点'(22,2)P,则点'P在平面内的射影P的坐标为;(Ⅱ)已知平面内的曲线'C的方程是222220xy,则曲线'C在平面内的射影C的方程是.评注本题是立体几何与平面解析几何交汇考查的典范,对空间想象能力提出较高的要求,同时也充分考查了解析几何的本质思想——几何问题代数化思想,是一个难得的好题.3.1空间想像能力空间想像能力是对空间形式的观察、分析、抽象的能力,主要表现为识图、画图和对图形的想像能力.评注本题以圆锥曲线为载体考查了类比推理、归纳推理、演绎推理以及证明方法,重点考查了抽象概括能力.在近年的试题中,以类比推理、归纳推理为基础、考查从归纳、猜想到论证的证明题崭露头角,这就对解题者提出了更高的素质要求.3.2抽象概括能力抽象概括能力就是从具体的、生动的实例,在抽象概括的过程中,发现研究对象的本质;从给定的大量信息材料中,概括出一些结论,并能应用于解决问题或作出新的判断.评注本题主要考查抛物线几何性质,直线与抛物线、点与圆的位置关系等知识,重点考查运算求解能力、推理证明能力.实质上,推理的过程隐含运算求解,运算求解的过程本身也是一种推理.3.3推理论证能力中学数学的推理论证能力是根据已知的事实和已获得的正确数学命题来论证某一数学命题真实性初步的推理能力.3.4运算求解能力运算能力包括分析运算条件、探究运算方向、选择运算公式、确定运算程序等一系列过程中的思维能力,也包括在实施运算过程中遇到障碍而调整运算的能力.3.4运算求解能力3.4运算求解能力3.4运算求解能力3.4运算求解能力3.4运算求解能力评注本题考查求椭圆的标准方程,直线与椭圆的位置关系等知识点,考查函数与方程思想、数形结合思想、化归与转化思想,考查运算求解能力、推理论证能力.第一小题的解法1:利用椭圆的定义求椭圆的标准方程,解法2:利用待定系数法求椭圆的标准方程.第二小题的解法1、2:利用函数方程的思想,解法3:利用椭圆的参数方程,解法4是:利用柯西不等式,解法5:利用数形结合.在上述众多解法的选择中,学生需...