高中数学 正弦函数、余弦函数的性质课件16 新人教A版必修4 课件VIP免费

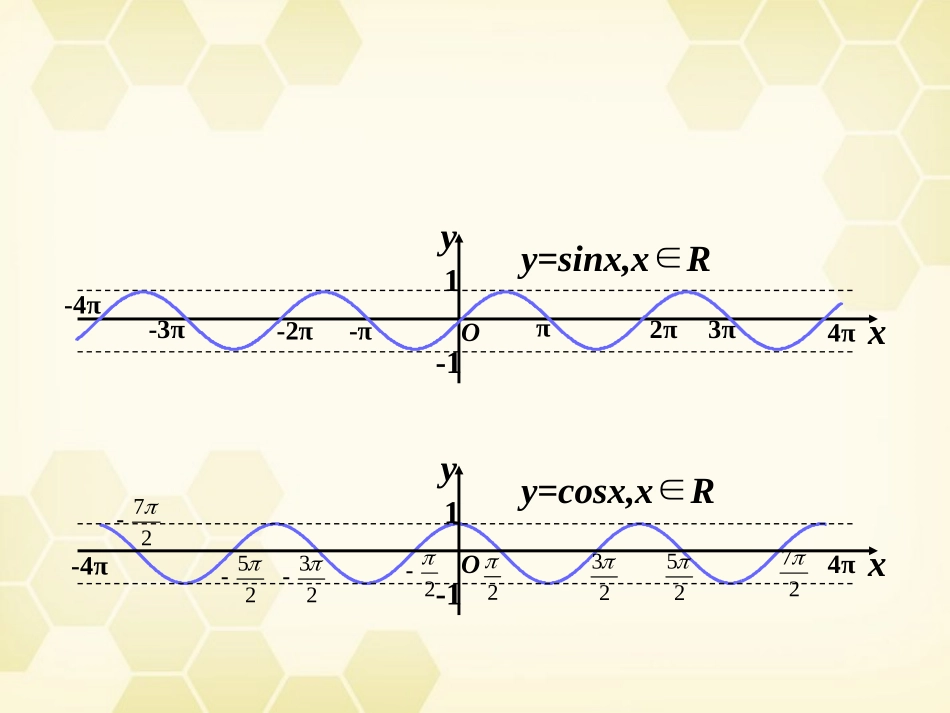
正弦函数、余弦函数的性质y=sinx,x∈RxyO-11π2π-π-2π-3π3π4π-4πyy=cosx,x∈RxO-114π-4π25232722327252(1)周期性对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有f(x+T)=f(x)那么函数f(x)就叫做周期函数.非零常数T叫做这个函数的周期.正弦函数是周期函数,2kπ(k∈Z且k≠0)都是它的周期,最小正周期是2π.y=sinx,x∈RxyO-11π2π-π-2π-3π3π4π-4πyy=cosx,x∈RxO-114π-4π25232722327252余弦函数是周期函数,2kπ(k∈Z且k≠0)都是它的周期,最小正周期是2π.例2求下列函数的周期:13cos,;2sin2,;132sin,.26yxxRyxxRyxxR解:(1)因为3cos(x+2π)=3cosx所以由周期函数的定义可知,原函数的周期为2π(2)因为sin2(x+π)=sin(2x+2π)=sin2x,所以由周期函数的定义可知,原函数的周期为π所以由周期函数的定义可知,原函数的周期为4π12sin426x12sin226x1=2sin26x例2求下列函数的周期:13cos,;2sin2,;132sin,.26yxxRyxxRyxxR3cos,;sin2,;12sin,.26yxxRyxxRyxxRπ2π4π这些函数的周期与解析式中哪些量有关?与自变量的系数有关31sin,;42cos4,;13cos,;214sin,.34yxxRyxxRyxxRyxxR求下列函数的周期练习83T2T2T6T探究函函ysinx函函函ycosx函函函函函函函函函≠0,函函函函函函函函函函函函函函函函函函函函函函函函函函函函函函函函函令z=xz∈Ry=Asinz,zR∈及y=Asinz,z∈R的周期都是2π222zxx自变量x只要并且至少要增加到2x函数值才能重复出现2T是使等式sinsin,coscos,AxTAxAxTAx成立的最小正数2T函函ysinxxR∈函函函ycosxxR∈函函函思考“如果函数y=f(x)的周期是T,那么函数y=f(ωx)的周期是”能否成立？T令z=ωx有y=f(z)且周期为TTxTxTzTzfzfTfxfxy=f(ωx)的周期是T(2)奇偶性正弦函数是奇函数y=sinx,x∈RxyO-11π2π-π-2π-3π3π4π-4πyy=cosx,x∈RxO-114π-4π25232722327252关于原点对称关于y轴对称sin(-x)=-sinx余弦函数是偶函数cos(-x)=cosx(3)单调性x···0······π···sinx3222yxO1-12232-1↘0↘1↗0↗-1正弦的一个周期上23,2正弦函数在每一个闭区间2,222kkkZ上都是增函数,其值从-1增大到1;在每一个闭区间32,222kkkZ上都是减函数,其值从1减小到-1x-π······0······πsinx22余弦的一个周期上[-π,π]yxO1-122-1↘0↘1↗0↗-1余弦函数在每一个闭区间2,2kkkZ上都是增函数,其值从-1增大到1;在每一个闭区间上都是减函数,其值从1减小到-12,2kkkZ(4)最大值与最小值正弦函数当且仅当x=_____________时取得最大值1,当且仅当x=_____________时取得最小值-1;余弦函数当且仅当x=_____________时取得最大值1,当且仅当x=_______________时取得最小值-1.22kkZ22kkZ2kkZ2kkZ例3下列函数有最大值、最小值吗?如果有,请写出取最大值、最小值时的自变量x的集合,并说出最大值、最小值分别是什么.(1)y=cosx+1,x∈R;(2)y=-3sin2x,x∈R.解:(1)使函数y=cosx+1,x∈R取得最大值的x的集合,就是使函数y=cosx,x∈R取得最大值的x的集合{x|x=2kπ,kZ}∈取最小值时x的集合{x|x=(2k+1)π,kZ}∈(2)令z=2x,使函数y=-3sinz,z∈R取得最大值的z的集合是|2,2zzkkZ...