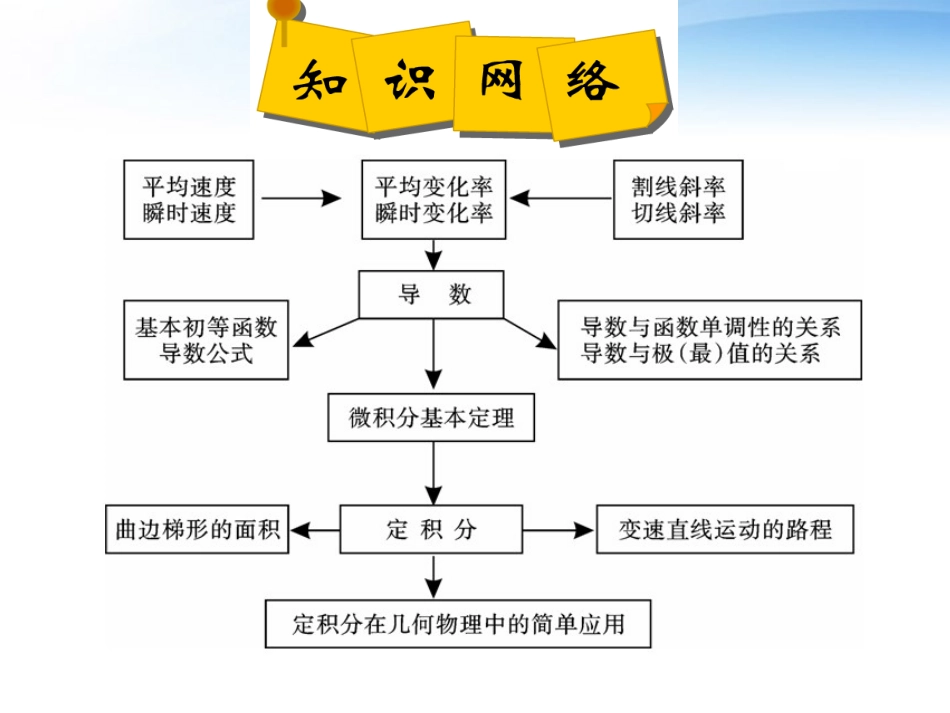
导数(含积分)的运算与应用知识梳理基础练习能力提升【考纲下载】1.了解函数单调性和导数的关系;能利用导数研究函数的单调性,会求函数的单调区间(其中多项式函数一般不超过三次).2.了解函数在某点取得极值的必要条件和充分条件;会用导数求函数的极大值、极小值(其中多项式函数一般不超过三次);会求闭区间上函数的最大值、最小值(其中多项式函数一般不超过三次).3.会利用导数解决某些实际问题.4.会计算常见函数的定积分,利用定积分会求曲边图形的面积.一、知识梳理一、知识梳理'()0,fx'()0fx0()()fxfx0()()fxfx二、基础练习二、基础练习BReturn三、能力提升三、能力提升题型三:已知函数的单调区间,求参数的范围.(高考命题研究专家原创卷)已知f(x)=xlnx,g(x)=-x2+ax-3.(1)求函数f(x)在[t,t+2](t>0)上的最小值;(2)对一切x∈(0,+∞),2f(x)≥g(x)恒成立,求实数a的取值范围;(3)证明对一切x∈(0,+∞),都有lnx>成立.思路点拨:(1)求出f′(x),对t进行讨论,(2)列出a的不等式,求a的取值范围转化成求函数的最值,(3)把不等式lnx>转化成xlnx>.证明xlnx的最小值不小于的最大值.解:(1)f′(x)=lnx+1,令f′(x)=0,则x=.当x∈时,f′(x)<0,f(x)单调递减,当x∈时,f′(x)>0,f(x)单调递增.①当00),则h′(x)=.当x∈(0,1)时,h′(x)<0,h(x)单调递减,当x∈(1,+∞)时,h′(x)>0,h(x)单调递增.所以h(x)min=h(1)=4.因为对一切x∈(0,+∞),2f(x)≥g(x)恒成立,所以a≤h(x)min=4.(3)问题等价于证明xlnx>(x∈(0,+∞)),由(1)知f(x)=xlnx(x∈(0,+∞))的最小值是-,当且仅当x=时取到.设m(x)=(x∈(0,+∞)),则m′(x)=,易得m(x)max=m(1)=-,当且仅当x=1时取到.从而对一切x∈(0,+∞),都有lnx>成立.导数的应用举例证:(1)∵x1时,g(x)>0,∴g(x)在(1,+∞)上为增函数.又g(x)在x=1处连续,∴f(x)=lnx<2.已知函数f(x)=lnx.(1)求证:当1a>0时,恒有ax<<.x-a2-f(x)2+f(x)f(x)-f(a)x+a22-f(x)2+f(x)∴要证x<成立,即lnx>成立.x+12(x-1)记g(x)=lnx-.x+12(x-1)则g(x)=-(x+1)241x只要证明x(2-lnx)<2+lnx,x(x+1)2(x-1)2=.∴g(x)>g(1)=0.∴lnx>成立.x+12(x-1)∴当1成立.x+12(x-1)∵当x>a>0时,>1,ax∴ln>.axax+12(-1)ax∴lnx-lna>.x+a2(x-a)lnx-lnax-a∴<,x+a2记h(x)=lnx-,xx-1则h(x)=xx-(x-1)212x-af(x)-f(a)即<.x+a2∴h(x)0,m2x32x2-mx+mn=x(x-m)+mn>0,x+mn>0.∴由f(x)<0得m≤x0得mn2,t=-.1mx2n∴由t<0得m≤x0得mn0,5+125-12∴h(u)在(1,2]上是增函数.=42-5.故对任意x1,x2[m,n),|f(x1)-f(x2)|≤42-5恒成立.∴h(u)≤h(2)=4-8+42-1变式:2(1)'()422()[1,1]'()0[1,1].220[1,1]1fxaxxfxfxxxaxx在上是增函,对恒成立即对恒成立[解析]20()212(1)1200012(1)1201011.axxaxaaaaaa设或或}.11|{,0)1(',10)1(',1],1,1[aaAfafax时以及当时只有当对[法一][法二]练习:可作多少条切线。过点)设(的单调增区间;求函数求的一个极值点是已知)5,2(,1)()(3)()2()1(ln22)(21xxfxgxfbxbxxfx变式: