高中数学 142 正弦函数、余弦函数的性质(2单调性等)课件 新人教A版必修4 课件VIP免费

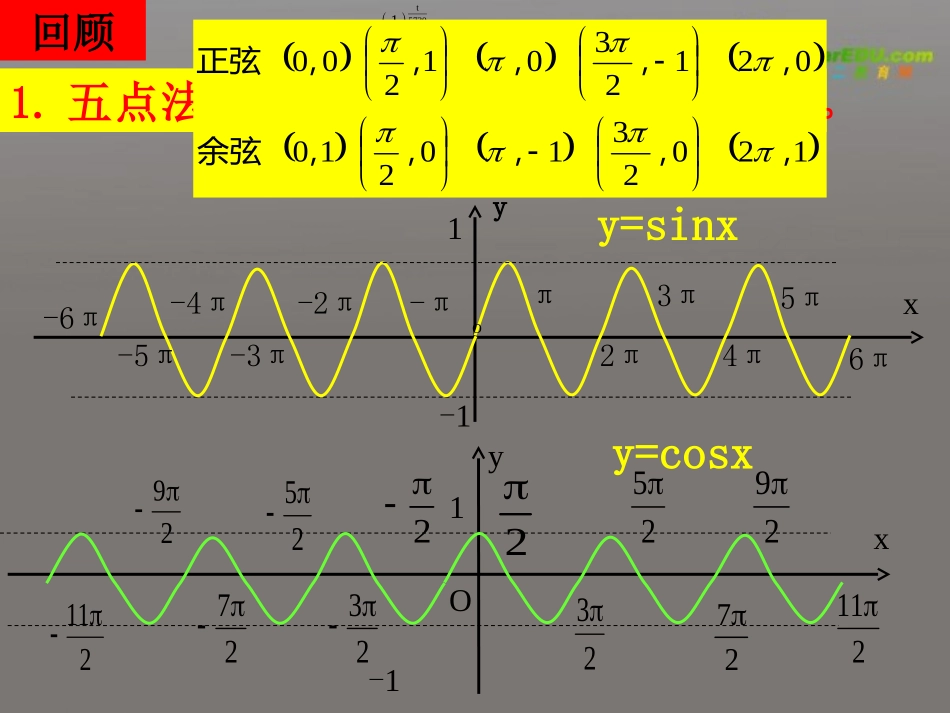
回顾t57301p21.五点法作正弦函数和余弦函数的图象。y-1xO1π2π3π4π5π6π-2π-3π-4π-5π-6π-πy=sinxxyO1-1222222222222y=cosx12023102100212301200，，，，，余弦，，，，，正弦对于函数对于函数f(x)f(x)，如果存在一个非，如果存在一个非零常数零常数TT，使得当，使得当xx取定义域内的每取定义域内的每一个值时一个值时，都有，都有f(x+T)=f(x),f(x+T)=f(x),那么那么函数函数f(x)f(x)就叫做周期函数，非零常数就叫做周期函数，非零常数TT就叫做这个函数的周期就叫做这个函数的周期..2.周期函数定义正、余弦函数是周期函数，2kπ（k∈Z,k≠0）都是它的周期，最小正周期是2π．2cossin的周期是与xAyxAy周期函数应用练习：(口算)求下列函数的周期：3(1).sin(2).cos441(3).cos(4).sin234yxyxyxyx例1、已知定义在R上的函数f(x)满足f(x＋2)＋f(x)=0，试判断f(x)是否为周期函数？周期函数应用结论：定义在R上的函数f(x)满足f(x＋a)＋f(x)=0或f(x＋a)=-f(x)则f(x)是周期为2a2a的周期函数.例2、已知定义在R上的函数f(x)满足f(x＋1)=f(x－1)，且当x∈[0，2]时，f(x)=x－4，求f(10)的值.结论：定义在R上的函数f(x)满足f(x＋a)-f(x-b)=0或f(x＋a)=f(x-b)则f(x)是周期为a+ba+b的周期函数.周期函数应用探究（一）：正、余弦函数的奇偶性和单调性思考1：观察下列正弦曲线和余弦曲线，判断正、余弦函数奇偶性？y-1xO1π2π3π4π5π6π-2π-3π-4π-5π-6π-πy=sinxxyO1-1222222222222y=cosx结论:正弦函数是奇函数,余弦函数是偶函数.思考2：观察正弦曲线，正弦函数在哪些区间上是增函数？在哪些区间上是减函数？如何将这些单调区间进行整合？y-1xO1π2π3π4π5π6π-2π-3π-4π-5π-6π-πy=sinx正弦函数在每一个闭区间上都是增函数；在每一个闭区间上都是减函数.[222kk[222kk思考3：类似地，余弦函数在哪些区间上是增函数？在哪些区间上是减函数？余弦函数在每一个闭区间上都是增函数；在每一个闭区间上都是减函数.[22kk[22kkxyO1-1222222222222y=cosx思考4：正弦函数在每一个开区间（2kπ，＋2kπ）(k∈Z)上都是增函数，能否认为正弦函数在第一象限是增函数？2探究（二）：正、余弦函数的最值与对称性思考1：观察正弦曲线和余弦曲线，正、余弦函数是否存在最大值和最小值？若存在，其最大值和最小值分别为多少？思考2：当自变量x分别取何值时，正弦函数y=sinx取得最大值1和最小值－1？结论：正弦函数当且仅当时取最大值1,当且仅当时取最小值-12xk2xk思考3：当自变量x分别取何值时，余弦函数y=cosx取得最大值1和最小值－1？结论：余弦函数当且仅当时取最大值1,当且仅当时取最小值-1.2xk(21)xk思考4：根据上述结论，正、余弦函数的值域是什么？函数y=Asinωx（Aω≠0）的值域是什么？[-|A|，|A|]思考5：正弦曲线除了关于原点对称外，是否还关于其它的点和直线对称？y-1xO1π2π3π4π5π6π-2π-3π-4π-5π-6π-πy=sinx正弦曲线关于点和直线对称.0k，2xk思考6：余弦曲线除了关于y轴对称外，是否还关于其它的点和直线对称？xyO1-1222222222222y=cosx余弦曲线关于点和直线对称.02k，xk理论迁移例1求下列函数的最大值和最小值，并写出取最大值、最小值时自变量x的集合（1）y=cosx＋1，x∈R；（2）y=－3sin2x，x∈R.例3求函数，x∈[－2π，2π]的单调递增区间.1sin()23yx例2比较下列各组数的大小:(1)sin()sin();1810与2317(2)cos()cos().5与...