高中数学23等差数列的前n项和课件新人教A版必修5 课件VIP免费

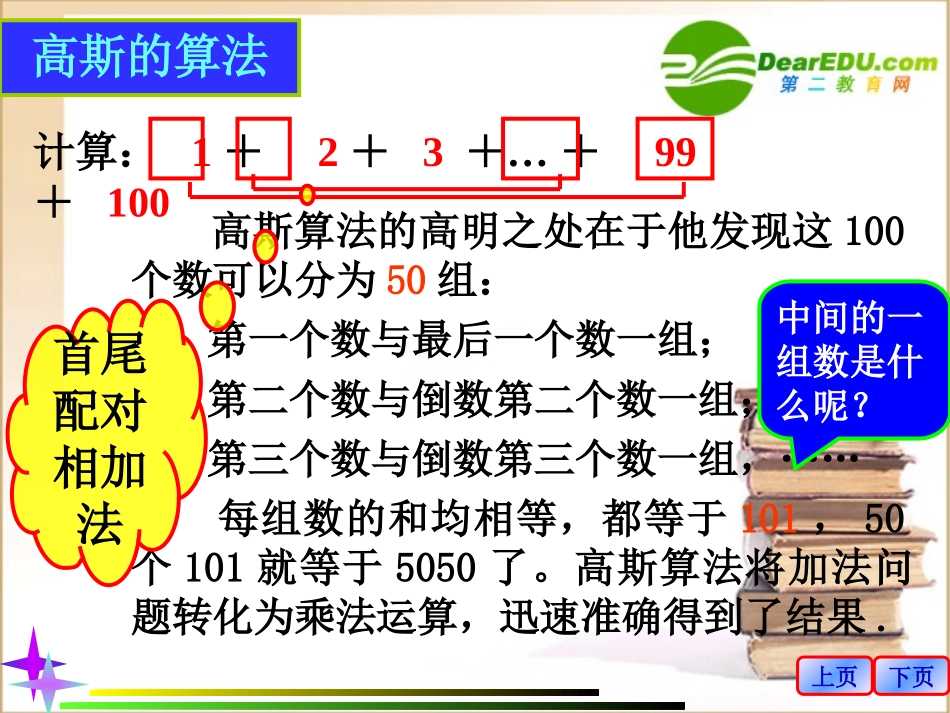
Microsoft公式3.0有一次，老师和高斯经过建筑工地，建筑工地上放着一堆圆木，从上到下每层的数目分别为1，2，3，……，100.老师问：高斯，你知道共有多少根圆木吗？问题就是：计算1＋2＋3＋…＋99＋100=？创设情景上页下页高斯的算法计算：1＋2＋3＋…＋99＋100高斯算法的高明之处在于他发现这100个数可以分为50组：第一个数与最后一个数一组；第二个数与倒数第二个数一组；第三个数与倒数第三个数一组，……每组数的和均相等，都等于101，50个101就等于5050了。高斯算法将加法问题转化为乘法运算，迅速准确得到了结果.首尾配对相加法中间的一组数是什么呢？下页上页nn)1(321计算：2)1()1(321nnnnn＋(n-1)＋(n-2)＋…＋2＋1(1)(1)...(1)(1)(1)nnnnnn分析：这其实是求一个具体的等差数列前n项和.①②启发倒序相加法上页下页探究高斯的算法妙处在哪里？这种方法能够推广到一般等差数列的前n项和吗？上页下页123nnSaaaa12()nnSnaa1213212nnnnnSaaaaaaaa121321nnnnaaaaaaaa又合作探究已知等差数列｛an｝的首项为a1，项数是n，第n项为aann，，求前求前nn项和项和SSnn..如何才能将等式的右边化简？121nnnnSaaaa1()2nnnaaS即①②思考：还有别的推导方法吗？上页下页已知等差数列｛an｝的首项为a1，项数是n，第n项为aann，，求前求前nn项和项和SSnn..111121aadadand21nnnnaadadand11()2(),2nnnnnaaSnaaS即2nS1naa1naa＋1naa＋＋…＋1naa123nnSaaaa121nnnnSaaaa又①②上页下页另解①+②得倒序相加法公式变形1()2nnnaaS1(1)naand把代入公式得1(1)2nnnSnad上页下页1()2nnnaaS等差数列的前n项和的公式：1(1)2nnnSnad含a1和d求和公式含a1和an1,,,5,nnadnas结构，应：由个元素用：可构成：知三求一公式记忆上页公式应用公式记忆对比：我们可结合梯形的面积公式来记忆等差数列前n项和公式.na1an1()2nnnaaSna1a1(n-1)d1(1)2nnnSnad将图形分割成一个平行四边形和一个三角形.下页返回公式应用11.15,95,10;2100,2,50;nnnSaanadnn根据下列条件，求出相应的等差数列{a}的前项和（）（）1()10(595)150022nnnaaS解：1(1)5049250100(2)222550nnnSnad解：上页下页例题讲解例1、2000年11月14日教育部下发了《关于在中小学实施“校校通”工程的通知》，某市据此提出了实施“校校通”工程的总目标：从2001年起用10年的时间，在全市中小学建成不同标准的校园网。据测算，2001年该市用于“校校通”工程的经费为500万元。为了保证工程的顺利实施，计划每年投入的资金都比上一年增加50万元。那么，从2001年起的未来10年内，该市在“校校通”工程中的总投入是多少？分析：①找关键句；②求什么，如何求？上页下页解：依题意得，该市在“校校通”工程的经费每年比上一年增加50万元，所以每年投入的资金构成等差数列{an}，且a1=500,d=50,n=10.1010101105005072502S万元那么，到2010年（n=10),投入的资金总额为答：从2001~2010年，该市在“校校通”工程中的总投入是7250万元.上页下页例题点评解决实际问题的步骤：（1）仔细阅读题目，审清题意；（2）提取相关数学信息，建立数学模型（本题为等差数列模型）；（3）解决此数学模型所体现的数学问题（本题是根据首项和公差选择前n项和公式进行求解）；（4）还原问题（回到实际问题中作答）。易错方面：（1）审题不清（如：把前n项和与最后一项混淆）（2）项数……（3）忘记答或写单位上页下页例题讲解例2、已知一个等差数列｛an｝的前10项的和是310，前20项的和是1220，由这些条件能确定这个等差数列的前n项和的公式吗？分析：方程思想和前n项和公式相结合解：由题意知：S10＝310，S20＝1220，将它们代入公式1(1)2nnn...