高中数学导数在求函数单调性中的应用优质课课件新人教A版选修2-2 课件VIP免费

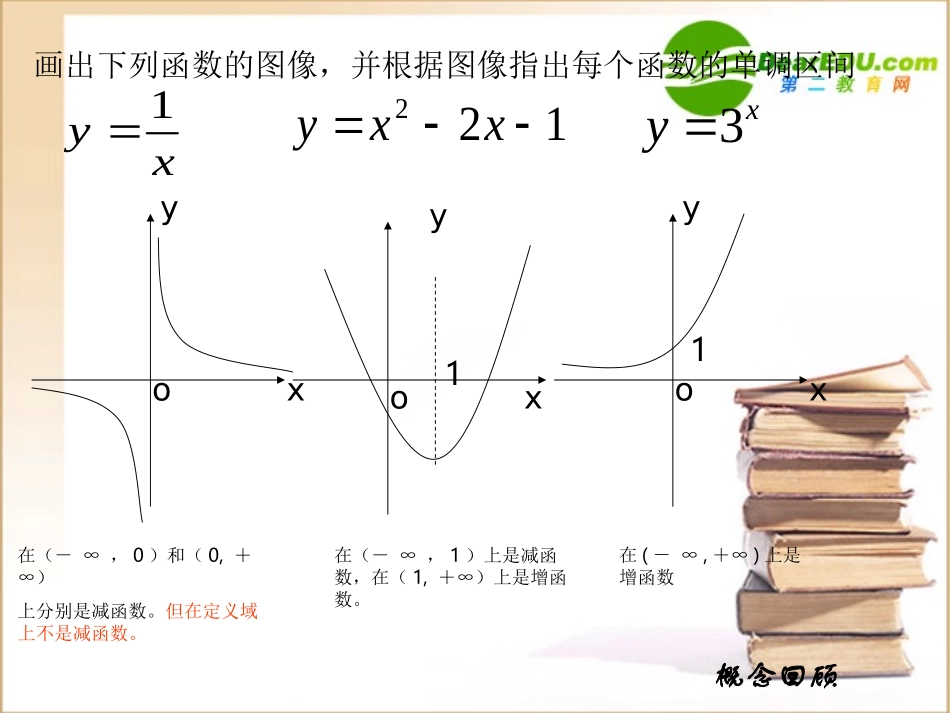
函数的单调性一.教学目标1.知识目标：掌握用导数的符号判别函数增减性的方法，提高对导数与微分的学习意义的认识。2.能力目标：训练解题方法，培养解题能力。3.德育目标：能用普遍联系的观点看待事物，抓住引起事物变化的主要因素。4.美育目标：数学方法的广泛应用之美，数学内容的统一性。二.教学重点：利用导数的符号确定函数的单调区间。三.教学难点：利用导数的符号确定函数的单调区间。情境设置探索研究演练反馈总结提炼作业布置创新升级oyxyox1oyx1xy1122xxyxy3在（－∞，0）和（0,＋∞）上分别是减函数。但在定义域上不是减函数。在（－∞，1）上是减函数，在（1,＋∞）上是增函数。在(－∞,＋∞)上是增函数概念回顾画出下列函数的图像，并根据图像指出每个函数的单调区间单调性的概念对于给定区间上的函数f(x):1.如果对于这个区间上的任意两个自变量x1,x2,当x1f(x2),那么就说f(x)在这个区间上是减函数（或单调递减函数）对于函数y＝f(x)在某个区间上单调递增或单调递减的性质，叫做f(x)在这个区间上的单调性，这个区间叫做f(x)的单调区间。ox1y1.在x＝1的左边函数图像的单调性如何？定理：一般地，函数y＝f（x）在某个区间内可导：如果恒有，则是增函数。如果恒有，则是减函数。如果恒有，则是常数。0)('xf)(xf0)('xf)(xf0)('xf)(xf新课引入首页2.在x＝1的左边函数图像上的各点切线的倾斜角为(锐角/钝角)?他的斜率有什么特征？3.由导数的几何意义，你可以得到什么结论？4.在x＝1的右边时，同时回答上述问题。例1.确定函数在哪个区间是减函数？在哪个区间上是增函数？54)(2xxxf2xyo解:(1)求函数的定义域函数f(x)的定义域是(－∞,＋∞)（2）求函数的导数42)('xxf（3）令以及求自变量x的取值范围，也即函数的单调区间。0)('xf0)('xf令2x－4>0,解得x>2∴x∈(2,＋∞)时，是增函数令2x－4<0,解得x<2∴x∈(-∞,2)时，是减函数)(xf)(xf练习确定函数，在哪个区间是增函数，那个区间是减函数。762)(23xxxfxyo解：函数f(x)的定义域是(－∞,＋∞)xxxf126)(2'令6x2－12x>0,解得x>2或x<0∴当x∈(2,＋∞)时，f(x)是增函数；当x∈(－∞，0)时，f(x)也是增函数令6x2－12x<0,解得,00以及f’(x)<0,求自变量x的取值范围，即函数的单调区间。f’(x)>0f’(x)<0f’(x)＝0首页例2.点p在曲线上移动，设点p处的倾斜角为，求的取值范围13xxy),43[)2,0[解：xxxxy14142'是减函数。上，和在或解得令是增函数。上，和在或解得令)()21,0()21,(21021014)(),21()0,21(021210)14(0142'22'xfxxxxyxfxxxxxxy提高题是减函数。上，在解得令是增函数。上，在或解得令解：定义域为)()21,0(2121014)(),21(2121014001402'22'xfxxxyxfxxxxxxyx求函数的单调区间。xxyln22单调区间的）（求函数设例)),0((,ln)(,04.xaxxxfa)0(,121)('xaxxxf解：aaaaxaxxfy144)42()42()(2222'考察函数0)42(0)(0)42(0)(0)42(0)(2201210)(0,022'22'22'axaxxfaxaxxfaxaxaxxxaxaxxxfxa同理即令是减函数）上在区间（解得令是增函数上）和在区间（或解得即令时，当)(122,122122122,0)()(),122(1220,1221220)42(,0)(,010)1'22'xfaaaaaaxaaxfxfaaaaaaxaaxaxaxxfa上单调递增在处连续在又上是递增）和在区间（，解得令时，当),0()(1)(,2ln1)1(),1(0,1)(10)()0(,)1(12)(1)2'22'xfxxffxfxxfxxxxxfa）上单调递增。在（恒成立即恒成立时，当0,)(0)(0)42(01)3'22xfxfaxaxa首页作业布置：书本P128习题3.61.2（3）（5）（6）同步练以及资源库相关题目