高中数学 31(空间向量及其运算)课件五 新人教A版选修2-1 课件VIP免费

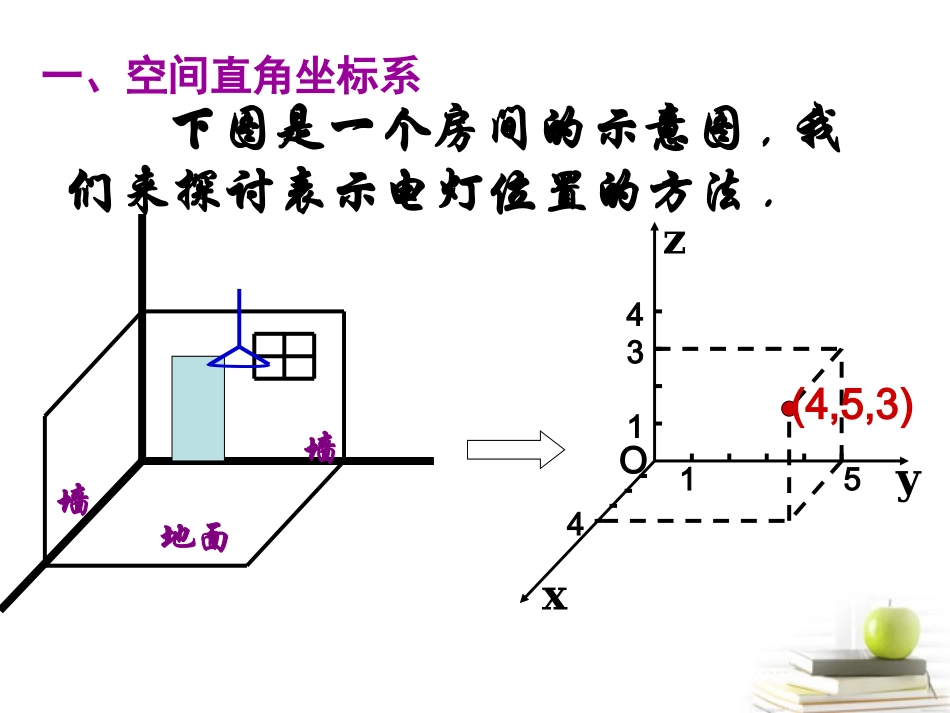
3.1.4空间向量的坐标表示提问:我们知道,在平面直角坐标系中,平面上任意一点的位置都有唯一的坐标来表示.那空间中任意一点的位置怎样用坐标来表示?墙墙地面下图是一个房间的示意图,我们来探讨表示电灯位置的方法.z134x4y15O(4,5,3)一、空间直角坐标系oxyz从空间某一个定点０引三条互相垂直且有相同单位长度的数轴，这样就建立了空间直角坐标系０－xyz．点Ｏ叫做坐标原点，x轴、y轴、z轴叫做坐标轴，这三条坐标轴中每两条确定一个坐标平面，分别称为xoy平面、yoz平面、和Zox平面．oxyz在空间直角坐标系中,让右手拇指指向x轴的正方向，食指指向y轴的正方向，若中指指向z轴的正方向，则称这个坐标系为右手直角坐标系．说明:☆我们一般建立的坐标系都是右手直角坐标系.空间直角坐标系的画法:oxyz1.X轴与y轴、x轴与z轴均成1350,而z轴垂直于y轴．135013502.y轴和z轴的单位长度相同，x轴上的单位长度为y轴（或z轴）的单位长度的一半．有了空间直角坐标系，那空间中的任意一点Ａ怎样来表示它的坐标呢？oxyzＡabc(a,b,c)经过A点作三个平面分别垂直于x轴、y轴和z轴，它们与x轴、y轴和z轴分别交于三点，三点在相应的坐标轴上的坐标a,b,c组成的有序实数对（a,b,c)叫做点Ａ的坐标记为：Ａ（a,b,c)在空间直角坐标系中，作出点（５,４,６）.例１分析：oxyzＯ从原点出发沿x轴正方向移动５个单位Ｐ1Ｐ1沿与y轴平行的方向向右移动４个单位Ｐ2Ｐ2沿与z轴平行的方向向上移动６个单位ＰＰ（５,４,６）Ｐ１５Ｐ2４６例２．如图，已知长方体ABCD-A`B`C`D`的边长为AB=12,AD=8,AA`=5.以这个长方体的顶点Ａ为坐标原点，射线AB,AD,AA`分别为x轴、y轴和z轴的正半轴,建立空间直角坐标系,求长方体各个顶点的坐标．xyzAOA`BB`CC`DD`在空间直角坐标系中,x轴上的点、xoy坐标平面内的点的坐标各有什么特点？),,(zyxMxyzo)0,0,(xP)0,,0(yQ),0,0(zR)0,,(yxA),,0(zyB),,(zoxC)0,0,0(O１．x轴上的点横坐标就是与x轴交点的坐标，纵坐标和竖坐标都是０．２．xoy坐标平面内的点的竖坐标为０，横坐标与纵坐标分别是点向两轴作垂线交点的坐标．单位正交基底：如果空间的一个基底的三个基向量互相垂直，且大小都为1，那么这个基底叫做单位正交基底，常用来表示.{,,}ijk��ik�j有序实数组(,,)xyz一一对应pxiyjzk�,,ijk��为基底空间向量p�因此我们可以类似平面直角坐标系,建立空间直角坐标系在空间选定一点O和一个单位正交基底以点O为原点，分别以的正方向建立三条数轴：x轴、y轴、z轴，这样就建立了一个空间直角坐标系O—xyz.x轴、y轴、z轴，都叫做叫做坐标轴,点O叫做原点，向量都叫做坐标向量.通过每两个坐标轴的平面叫做坐标平面.{,,}ijk��,,ijk��,,ijk��123(,,)AaaaaxyzOkij对空间任一向量,由空间向量基本定理，存在唯一的有序实数组,使a123(,,)aaa123.aaiajak��有序实数组123(,,)aaa就叫做a在这一空间直角坐标系下的坐标.记为123(,,)aaaa.空间直角坐标系在空间直角坐标系O–xyz中，对空间任一点A,对应一个向量,于是存在唯一的有序实数组x,y,z,使(如图).OA�OAxiyjzk�显然,向量的坐标，就是点A在此空间直角坐标系中的坐标(x,y,z).OA�xyzOA(x,y,z)ijk即(,,)(,,)OAxyzAxyz�也就是说,以O为起点的有向线段(向量)的坐标可以和点的坐标建立起一一对应的关系,从而互相转化.我们说,点A的坐标为(x,y,z),记作A(x,y,z)，其中x叫做点A的横坐标,y叫做点A的纵坐标,z叫做点A的竖坐标.空间向量运算的坐标规律:,则设123123(,,),(,,)aaaabbbbababa//ab112233(,,)ababab112233(,,)ababab123(,,)()aaaR112233,,()abababR练习1:已知求),4,1,3(),5,3,2(babaababa,8,,(2,3,5)(3,1,4)(1,2,1)ab(2,3,5)(3,1,4)(5,4,9)ab88(2,3,5)(16,24,40)a(2,3,5)(3,1,4)29ab解:结论：若A(x...