高中数学 第二章 平面向量知识素材 新人教A版必修4 素材VIP免费

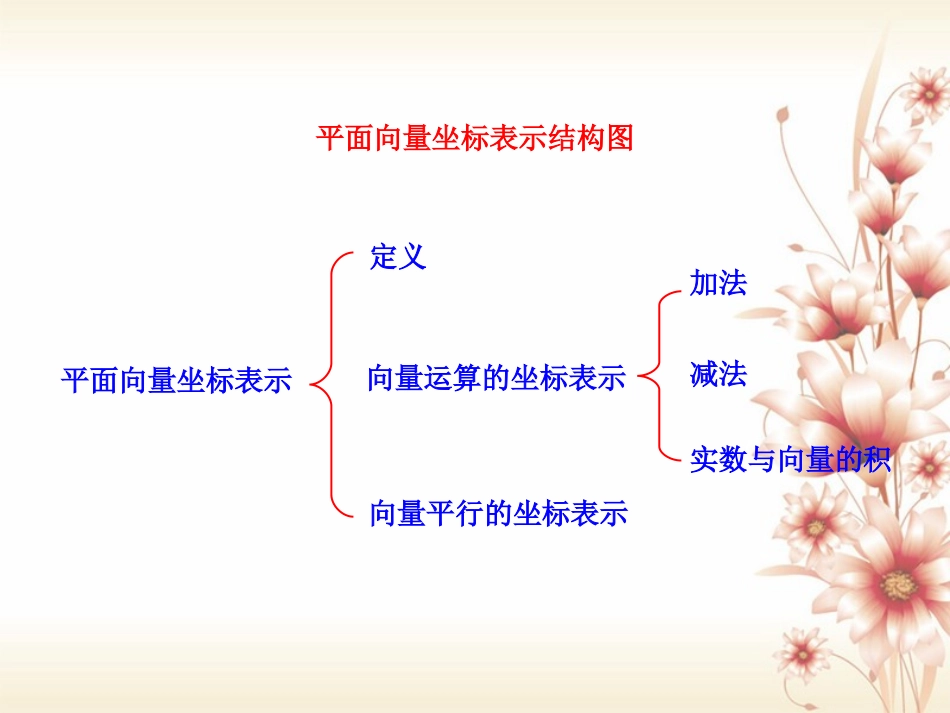
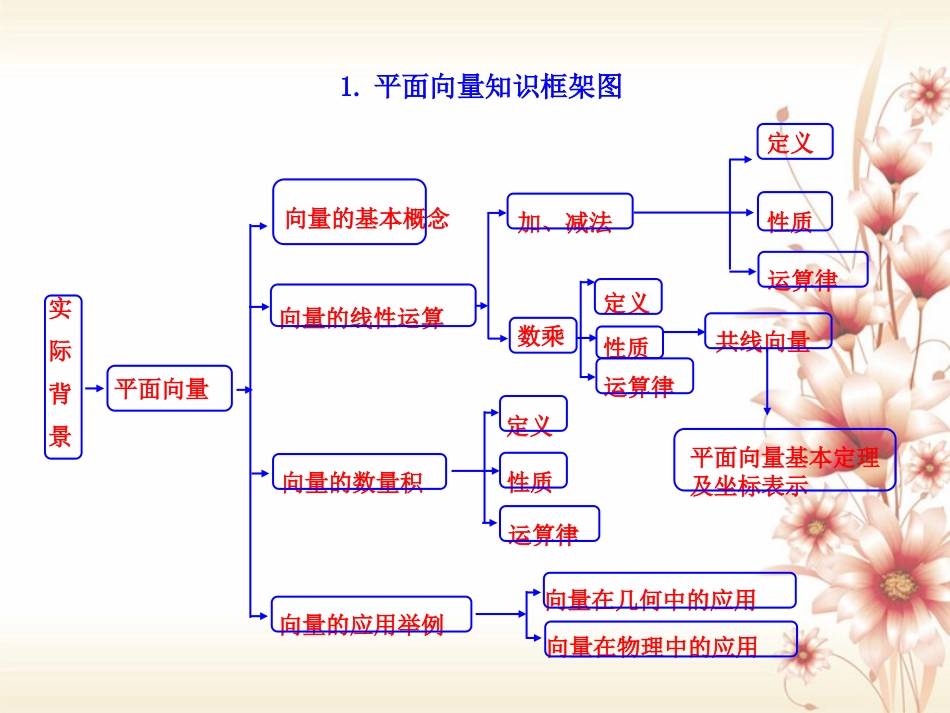
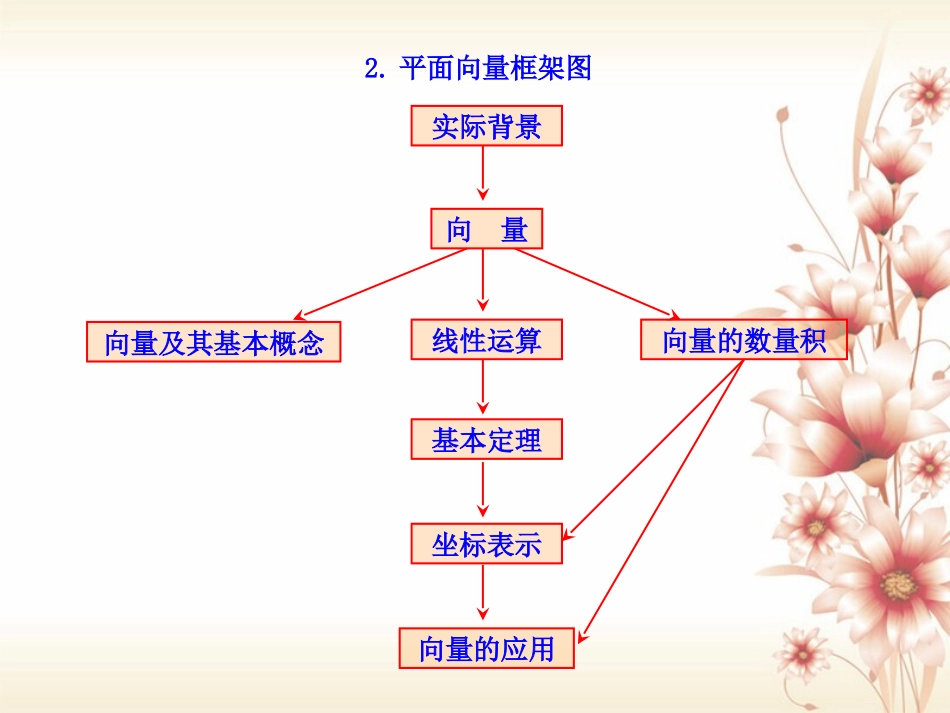
平面向量坐标表示结构图平面向量坐标表示定义向量运算的坐标表示向量平行的坐标表示加法减法实数与向量的积1.平面向量知识框架图实际背景平面向量加、减法数乘定义性质运算律定义性质运算律定义性质运算律共线向量平面向量基本定理及坐标表示向量在几何中的应用向量在物理中的应用向量的基本概念向量的线性运算向量的数量积向量的应用举例向量及其基本概念线性运算向量的数量积基本定理坐标表示向量的应用向量实际背景2.平面向量框架图向量A(起点)B(终点)相等向量ab数量积ABOB1bcosba向量加法的三角形法则ABCababab向量加法的平行四边形法则ABCOabab1.向量加法的运算法则向量求和的法则三角形法则平行四边形法则运算律交换律结合律a+b=b+aa+b+c=a+b+c已知非零向量在平面内任取一点A，作则向量叫做与的和，记作，即这种求向量和的方法，称为向量加法的三角形法则，，abABBC�，，abababABBC��abAC.�AC�已知两个不共线向量作则A，B，D三点不共线，以AB，AD为邻边作平行四边形ABCD，则对角线上的向量如图.这种作两个向量和的方法叫做向量加法的平行四边形法则，，abAB�，aAD�，bAC�，a+b2.向量的减法定义几何意义向量加上向量的相反向量,叫做的差,即求两个向量差的运算,叫做向量的减法ab与ab（）ab=a+b,如图,设可以表示为从向量的终点指向向量的终点的向量OA,OB,BA,�则即abababba3.三角形法则与平行四边形法则的区别适用条件作图时的要求三角形法则平行四边形法则法则注意问题内容任意向量求和首尾相接不共线的向量求和起点重合1.平面向量基本定理平面向量基本定理定理基底如果是同一平面内的两个不共线向量，那么对于这一平面内的任意向量有且只有一对实数使.12ee�，a，12,，1122aee��不共线的向量叫做表示这一平面内所有向量的一组基底.12e,e�2.平面向量的坐标运算向量的加、减法实数与向量的积向量的坐标aa若=（x,y），λ∈R，则=（λx，λy），即实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标即两个向量和（差）的坐标分别等于这两个向量相应坐标的和（差）1122a(xy)b(xy)若＝，，，，ab,则1212ab(xx,yy)，1212xxyy（，）已知向量的始点A（x1，y1），终点B（x2，y2），则（x2-x1，y2-y1），即一个向量的坐标等于表示此向量的有向线段的终点的坐标减去始点的坐标AB�AB�用向量方法解决平面几何问题的三个步骤建立平面几何与向量的联系，用向量表示问题中涉及的几何元素，将平面几何问题转化为向量问题通过向量运算，研究几何元素之间的关系，如距离、夹角等问题把运算结果“翻译”成几何关系转化运算翻译1.平面向量的数量积定义几何意义已知两个非零向量与，我们把数量叫做与的数量积.记作，即，其中θ是与的夹角，零向量与任一向量的数量积为0ab|a||b|cosababab|a||b|cosab叫做向量在方向上（在方向上）的投影.的几何意义是数量积等于的长度与在的方向上的投影的乘积ab|a|cos(|b|cos)baababa|a|ba|b|cos性质运算律22ab(1)abab0(2)abab=|a||b|abab=|a||b|(3)aa|a||a|=aaaab(4)cos|a||b|(5)|ab||a||b|设和都是非零向量，则当与同向时，，当与反向时，或abba(a)b(ab)a(b)a(bc)abac交换律：结合律：分配律：与向量有关的概念名称定义备注零向量单位向量相等向量平行向量(共线向量)相反向量0a(a为任意向量）00长度为0的向量方向不确定,是任意的长度等于1个单位的向量长度相等且方向相同的向量方向相同或相反的非零向量长度相等，方向相反的向量2.三个重要公式三个重要公式向量模公式：设221111a(x,y),axy则两点间距离公式：若1122A(x,y),B(x,y)，222121AB(xx)(yy)�则向量的夹角公式：设两非零向量1122121222221122a(x,y),b(x,yabxxyyabcosabxyxy)，与的夹角为，则