高中数学 113(导数的几何意义)课件1 新人教B版选修2-2 课件VIP免费

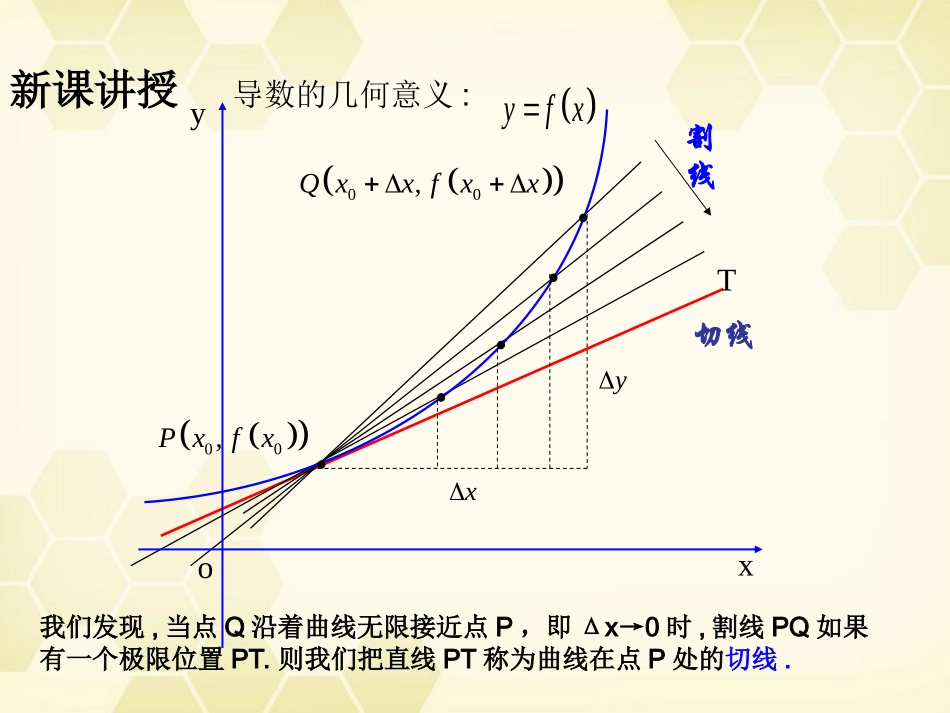
1.1.3导数的几何意义3.导数的定义4.点斜式直线方程：)(00xxkyy1.平均变化率0已知函数y=f(x)在点x=x及其附近有定义00叫做函数y=f(x)在x到x+x之间的平均变化率.00()()x0,fxxfxyxx当时比值'000)()()limxxfxfxx0f(x故00函数在x的瞬时变化率，就定义为f(x)在x=x处的导数0''0xxfxy记作或00()()0fxxfxxx当趋近于时，平均变化率2.瞬时变化率趋近于一个常数，这个常数称为函数在点的瞬时变化率fx0x复习回顾oxy割线切线T导数的几何意义:我们发现,当点Q沿着曲线无限接近点P，即Δx→0时,割线PQ如果有一个极限位置PT.则我们把直线PT称为曲线在点P处的切线.新课讲授00,Pxfx00,Qxxfxxyxyfx那么当Δx→0时,割线PQ的斜率趋向于过点P的切线PT的斜率即:'00000()()()limlimxxfxxfxykfxxx切线'000,.xxfxfx曲线y=f过点的切线的斜率由导数等于意义可知，割线切线T00,Pxfx00,Qxxfxxyxoxyyfx例1:求抛物线y=f(x)=x2在点P(1,1)处的切线的斜率.'02020:(1)(1)1lim(1)1lim2()lim2.xxxfxffxxxxxx解过点(1,1)切线的斜率是（）2112.x因此，抛物线y=f=x在点P，处的切线斜率为2yxyxo1,1P例题讲解例2.求双曲线过点的切线方程。1yx12,200112222.limlimxxfxfxxx解因为011lim224xx112.24所以，这条双曲线过点，的切线的斜率为-112,24x由直线方程的点斜式，得切线方程为y-11.4x即y=-yo●xyo12,2P练习:如图已知曲线,求:(1)点P处的切线的斜率;(2)点P处的切线方程.)38,2(313Pxy上一点3320011(2)233|limlimxxxxyyxx即点P处的切线的斜率等于4.(2).在点P处的切线方程是,即8423yx123160xyyx-2-112-2-11234OP313yx2301126()()lim3xxxxx201lim[126()]43xxx31(1),3yx解：253.6.2例求抛物线y=x过点，的切线方程200,.xx解：设此切线过抛物线上的点01.由例及导数的意义知此切线的斜率为2x20056x,,2x又因为此切线过点，和点200062,52xxx其斜率满足2000560,2,3.xx解得x22439.yx即切线过抛物线上的点，，，所以切线方程分别为：442,963.yxyx化简得y=4x-4,y=6x-9.2yxyxo5,62P2,43,9200,xx.2练习2174,.44yx求抛物线过点的切线方程（注意此点不在抛物线上）7177444242yxyx解：切线方程为或求过某点P曲线的切线方程的一般步骤：小结:（1）判断点P是否在曲线上。（2）若点P在曲线上，如例1，例2做法。（3）若点P不在曲线上，如例3，设出切点坐标，利用切线的斜率，求出切点的坐标。代入点斜式，求出切线的方程。。，，）（习题作业：321A1-3.85.P300x曲线y=x在处的切线是否存在，若存在，求出切线的斜率和切线方程；若不存在，请说明理由。思考题：