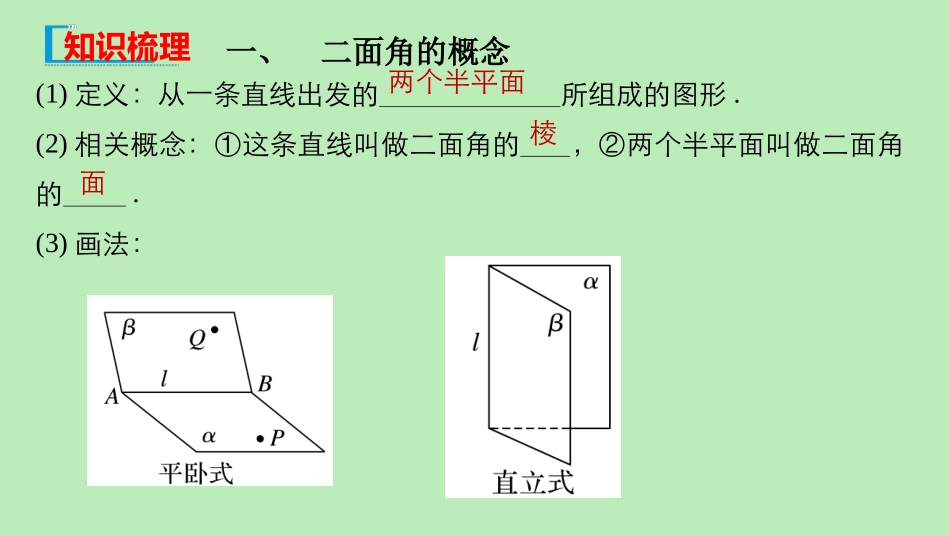
8.6.3平面与平面垂直学习目标1.理解二面角、二面角的平面角的概念.2.理解两个平面垂直的定义.3.理解平面与平面垂直的判定定理.4.能运用定理证明一些平面与平面垂直的问题.5.理解平面与平面垂直的性质定理,并能够证明.6.能运用性质定理证明一些空间位置关系的简单命题.重点:直观感知、操作确认,概括出面面垂直的判定定理、性质定理..难点:面面垂直判定定理的应用及二面角的求法,性质定理的证明.(1)定义:从一条直线出发的所组成的图形.(2)相关概念:①这条直线叫做二面角的,②两个半平面叫做二面角的.(3)画法:两个半平面棱面一、二面角的概念知识梳理(4)记法:二面角或或或P-AB-Q.(5)二面角的平面角:若有①Ol;②OAα,OBβ;③OAl,OBl,则二面角α-l-β的平面角是.α-l-βα-AB-βP-l-Q∈⊂⊂⊥⊥∠AOB(1)平面与平面垂直①定义:一般地,两个平面相交,如果它们所成的二面角是,就说这两个平面互相垂直.②画法:直二面角③记作:.α⊥β二、平面与平面垂直(2)判定定理文字语言一个平面过另一个平面的,则这两个平面垂直图形语言符号语言l⊥α,⇒α⊥β垂线l⊂β文字语言两个平面垂直,则垂直于的直线与另一个平面______符号语言α⊥β,α∩β=l,,⇒a⊥β图形语言一个平面内交线垂直a⊂αa⊥l三、平面与平面垂直的性质定理例1一求二面角常考题型[2019·重庆高一联考]如图,在正方体ABCD-A1B1C1D1中,求二面角B-A1C1-B1的正切值.【解】如图,取A1C1的中点O,连接B1O,BO,由题意知B1O⊥A1C1.又BA1=BC1,O为A1C1的中点,所以BO⊥A1C1,所以∠BOB1是二面角B-A1C1-B1的平面角.因为BB1⊥平面A1B1C1D1,OB1平面A1B1C1D1,所以BB1⊥OB1.设正方体的棱长为a,则OB1=22a.在Rt△BB1O中,tan∠BOB1=11BBOB=22aa=2,所以二面角B-A1C1-B1的正切值为2.◆求二面角的平面角的步骤(1)作:找出或作出二面角的平面角.(2)证:证明所找或所作的角就是二面角的平面角.(3)求:在三角形中解出角的大小.◆对于二面角及其平面角的理解:(1)二面角的平面角的大小由二面角的两个面的位置唯一确定,与棱上点的选择无关.(2)构成二面角的平面角的三要素:棱上、面内、垂直.即二面角的平面角的顶点必须在棱上,角的两边必须分别在两个半平面内,角的两边必须都与棱垂直.这三个条件缺一不可.前两个要素决定了二面角的平面角在同一个平面内,第三个要素决定了二面角的平面角大小的唯一性和平面角所在的平面与棱垂直.(3)二面角的平面角的范围是[0,π].训练题[2019·江西赣州二模]如图所示,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A和B的一点,且PA=AC,求二面角P-BC-A的大小.解: PA⊥平面ABC,BC平面ABC,∴PA⊥BC. AB是⊙O的直径,且点C在圆周上,∴AC⊥BC. PA∩AC=A,∴BC⊥平面PAC. PC平面PAC,∴PC⊥BC,∴∠PCA是二面角P-BC-A的平面角.由PA=AC知△PAC是等腰直角三角形,∴∠PCA=45°,即二面角P-BC-A的大小是45°.二平面与平面垂直的判定定理及应用例2[2019·广州越秀区校级检测]如图,在矩形ABCD,CDEF中,AB=2AD,ED=2AD,现以EC为折痕将△EFC折起,使点F落在AB上,位置记为点M.(1)证明:平面ABCD⊥平面CDEF.(2)若AB=2,求点B到平面MEC的距离.(1)【证明】设AD=m,则AB=CD=EF=2m,ED=CF=2m,由题意知CM=CF=2m,EM=EF=2m,在Rt△CBM中, BM=22CMCB=m,∴AM=AB-BM=m,DM2=AD2+AM2=2m2.在△EDM中, EM2=ED2+DM2,∴ED⊥DM. 四边形CDEF是矩形,∴ED⊥CD. CD∩DM=D,∴ED⊥平面ABCD. ED平面CDEF,∴平面ABCD⊥平面CDEF.(2)【解】由题意可得BM=1,BC=1,CM=2,ED=2,EM=2,由(1)知平面ABCD⊥平面CDEF,ED⊥平面ABCD.设点B到平面MEC的距离为d,由VE-CBM=VB-ECM,得13×12×BM×BC×ED=13×12×EM×CM×d=13×12×1×1×2=13×12×2×2×d,解得d=12,故点B到平面MEC的距离为12.◆证明面面垂直的方法(1)利用定义:证明二面角的平面角为直角.步骤:①找出两个相交平面的平面角;②证明这个平面角是直角;③根据定义,说明这两个平面互相垂直.(2)利用判定定理:证明一个平面经过另...