高中数学 圆与圆的位置关系课件 苏教版必修2 课件VIP免费

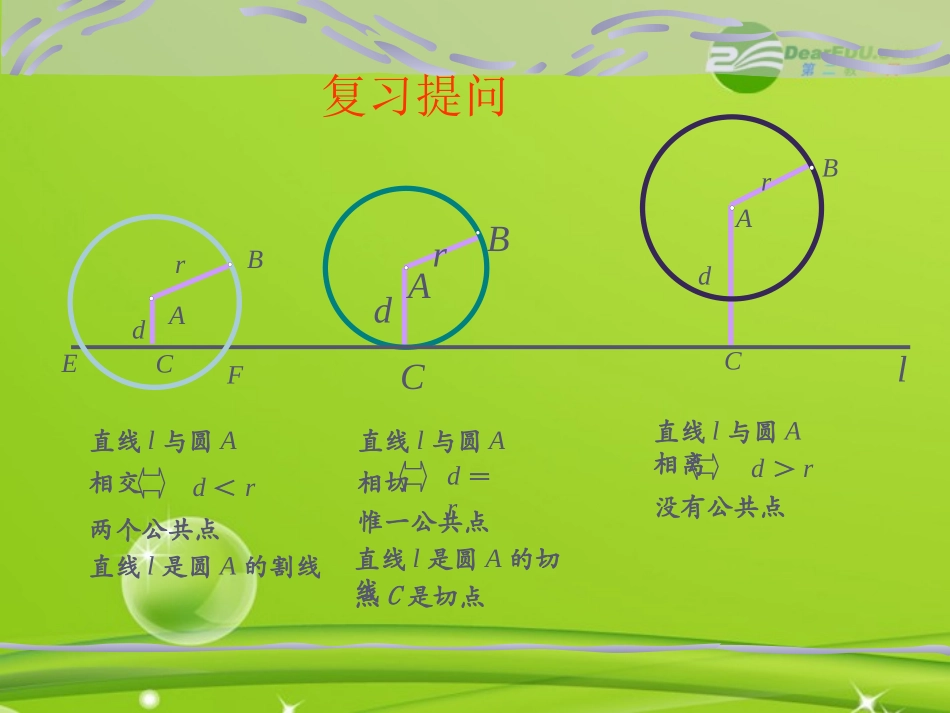
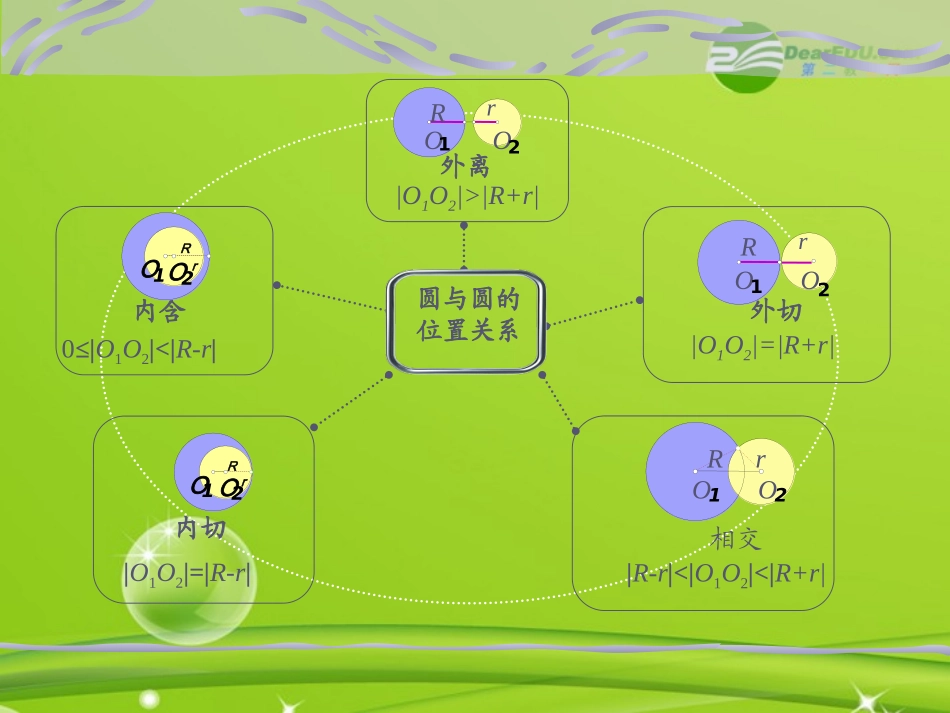
2.2.2圆与圆的位置关系复习提问直线l与圆A相交d＜r直线l是圆A的割线两个公共点dCrABdCrABl直线l与圆A相离d＞r没有公共点直线l是圆A的切线直线l与圆A相切d＝r惟一公共点点C是切点CFrABEd圆与圆的位置关系|O1O2|=|R-r|内切rRO1O2外离|O1O2|>|R+r|rRO1O20≤|O1O2|<|R-r|内含rRO1O2外切rRO1O2|O1O2|=|R+r|相交|R-r|<|O1O2|<|R+r|rRO1O2知识点拨1d=R-r内切公切线的条数d与R，r的关系图形两圆的位置关系00≤dR+r外离例1设圆C1:x2+y2+2x+8y-8=0,圆C2:x2+y2-4x-4y-2=0,试判断圆C1与圆C2的关系.xyABOC1C2①-,②得x+2y-1=0,由③,得解法一：圆C1与圆C2的方程联立,得到方程组①②22222880,4420,xyxyxyxy12,xy把上式代入①,并整理,得2230.xx方程④的判别式22413160,所以,方程④有两个不相等的实数根x1,x2分别代入方程③,得到y1,y2.因此圆C1与圆C2有两个不同的公共点A(x1,y1),B(x2,y2).③解法二:把圆C1的方程化为标准方程，得圆C1的圆心是点（-1，-4）,半径长r1=5.把圆C2的方程化为标准方程，得圆C1的圆心是点（2，2）,半径长r2=.圆C1与圆C2的连心线长为圆C1与圆C2的半径之和是两半径之差是所以圆C1与圆C2相交,他们有两个公共点A,B.221425.xy222210.xy1012510,rr22124235,12510,rr121251035510,35rrrr而即，小结：研究两圆的位置关系可以有两种方法:一是几何法,判断圆心距与两圆半径的和与差的绝对值的大小关系.一是代数法,联立两者方程看是否有解.1.点M在圆心为C1的圆x2+y2+6x-2y+1=0上,点N在圆心为C2的圆x2+y2+2x+4y+1=0上,求|MN|的最大值.yxOMNC1C2解:把圆的方程都化成标准形式,为(x+3)2+(y-1)2=9(x+1)2+(y+2)2=4如图,C1的坐标是(-3,1),半径3;C2的坐标是(-1,-2),半径是2,所以,|C1C2|==因此,|MN|的最大值是22)21()13(13.135.练一练：2.练习过两圆x2+y2+6x–4=0和x2+y2+6y–28=0的交点且圆心在直线x-y-4=0上的圆方程是()A.x2+y2-x-5y+2=0B.x2+y2-x-5y-2=0C.x2+y2-x+7y-32=0D.x2+y2+x+7y+32=0C