高三数学离散型随机变量的期望课件1 人教版 课件VIP免费

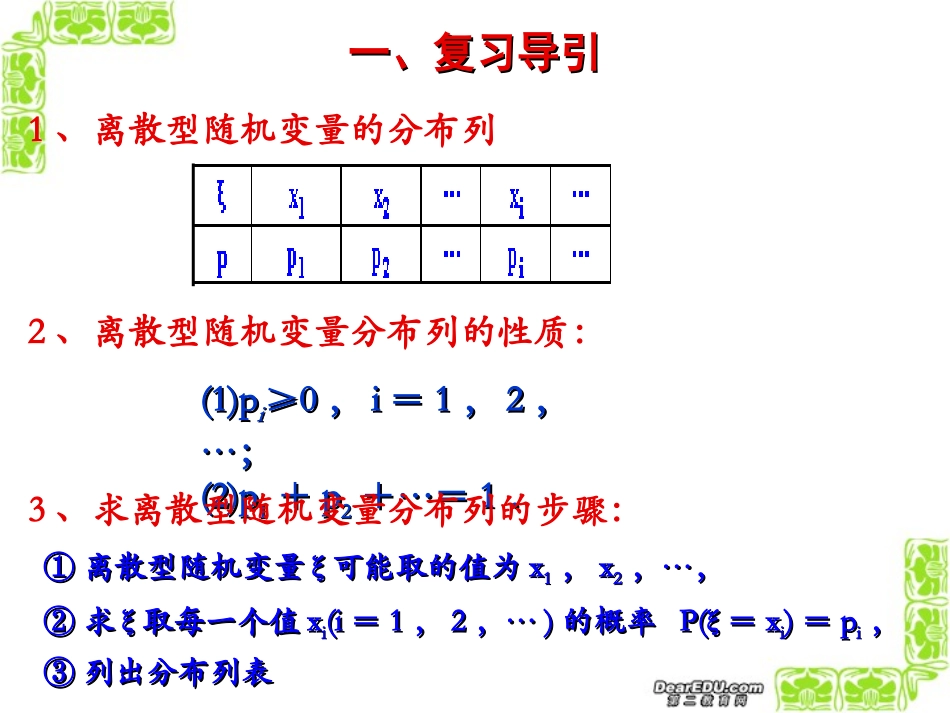
2、离散型随机变量分布列的性质：(1)p(1)pii≥0≥0，，ii＝＝11，，22，，…；…；(2)p(2)p11＋＋pp22＋…＝＋…＝11．．1、离散型随机变量的分布列一、复习导引一、复习导引3、求离散型随机变量分布列的步骤：①①离散型随机变量离散型随机变量ξξ可能取的值为可能取的值为xx11，，xx22，…，，…，②②求求ξξ取每一个值取每一个值xxii(i(i＝＝11，，22，…，…))的概率的概率P(ξP(ξ＝＝xxii))＝＝ppii，，③③列出分布列表列出分布列表新課引入新課引入1、某班级有10位同学参加一次数学竞赛，成绩分别为97、95、95、92、92、92、92、91、91、91。求平均成绩是多少？9795959292929291919192.810X平均成绩为：12439795929110101010有何意义？？把成绩看成随机变量的概率分布列新課引入新課引入能否估计出该射手100次射击的平均环数？2、某射手射击所得环数ξ的分布列如下：P(ξ＝4)×100＝2次得4环P(ξ＝5)×100＝4次得5环P(ξ＝6)×100＝6次得6环P(ξ＝7)×100＝9次得7环……P(ξ＝10)×100＝22次得10环平均环数为：平均环数为：425456...10228.32100能否估计出该射手n次射击的平均环数？P(ξ＝4)×n＝0.02n次得4环P(ξ＝5)×n＝0.04n次得5环P(ξ＝6)×n＝0.06n次得6环P(ξ＝7)×n＝0.09n次得7环P(ξ＝10)×n＝0.22n次得10环(40.0250.0450.06...100.22)8.32nn4(4)5(5)...10(10)8.32PPPE一般地，若离散型随机变量ξ的概率分布为则ξ的数学期望（或平均数、均值）新课教学新课教学一、离散型随机变量取值的平均水平—一、离散型随机变量取值的平均水平—Eξ＝x1p1＋x2p2＋…＋xnpn＋…设设ηη＝＝aξaξ＋＋bb，其中，其中aa，，bb为常数，则为常数，则ηη也是随机变也是随机变量．量．（（11））ηη分布列是什么？分布列是什么？（（22））Eη=Eη=？？问题问题数学期望数学期望设η＝aξ＋b，其中a，b为常数，则η也是随机变量．其分布列为新课教学新课教学Eξ＝x1p1＋x2p2＋…＋xnpn＋…ξx1x2…xn…ηax1+bax2+b…axn+b…PP1P2…Pn…于是于是EηEη＝＝(ax(ax11＋＋b)pb)p11＋＋(ax(ax22＋＋b)pb)p22＋…＋＋…＋(ax(axnn＋＋b)pb)pnn＋＋……＝＝a(xa(x11pp11＋＋xx22pp22＋…＋＋…＋xxnnppnn＋…＋…))＋＋b(pb(p11＋＋pp22＋…＋…+p+pnn＋…＋…))＝＝aEξaEξ＋＋bb．．即E(aξ＋b)＝aEξ＋bηax1+bax2+b…axn+b…PP1P2…Pn…一般地，若离散型随机变量ξ的概率分布为则ξ的数学期望（或平均数、均值）一、离散型随机变量取值的平均水平——数学期望一、离散型随机变量取值的平均水平——数学期望Eξ＝x1p1＋x2p2＋…＋xnpn＋…二、数学期望的性质二、数学期望的性质即E(aξ＋b)＝aEξ＋b新课教学新课教学课堂练习课堂练习1、随机变量ξ的分布列是ξ135P0.50.30.2(1)则Eξ=.2、随机变量ξ的分布列是ξ4a910P0.30.1b0.22.4(2)若η=2ξ+1，则Eη=.5.8ξ47910P0.3ab0.2Eξ=7.5,则a=b=.0.40.13、篮球运动员在比赛中每次罚球命中得1分，罚不中得0分．已知某运动员罚球命中的概率为0.7，则他罚球1次的得分ξ的期望为．4、随机抛掷一个骰子，所得骰子的点数为随机变量ξ.(1)求抛掷骰子所得点数ξ的概率分布列ξ123456P1/61/61/61/61/61/6(2)求抛掷骰子所得点数ξ的期望0.70.7课堂练习课堂练习5、有一批数量很大的产品，其次品率是15％．对这批产品进行抽查，每次抽出1件，如果抽出次品，则抽查终止，否则继续抽查，直到抽出次品，但抽查次数最多不超过10次．求抽查次数ξ的期望(结果保留三个有效数字)．解：前k-1次取出正品而第k次(k＝1，2，…，9)取出次品的概率P(ξ＝k)＝0.85k-1×0.15，(k＝1，2，…，9)；需要抽查10次即前9次取出的都是正品的概率P(ξ＝10)＝0.859．由此可得ξ的概率分布如下：Eξ＝1×0.15＋2×0.1275＋…＋10×0.2316＝5.35．ξ12345678910P0.150.150.12750.12750.10840.10840.0920.0920.07830.07830.06660.06660.05660.05660.04810.04810.0400.040990.230.231616课堂练习课堂练习7、某商场的促销决策：统计资料表明，每年国庆节商场...