高三数学 第三节 三角函数图像与性质复习课件VIP免费

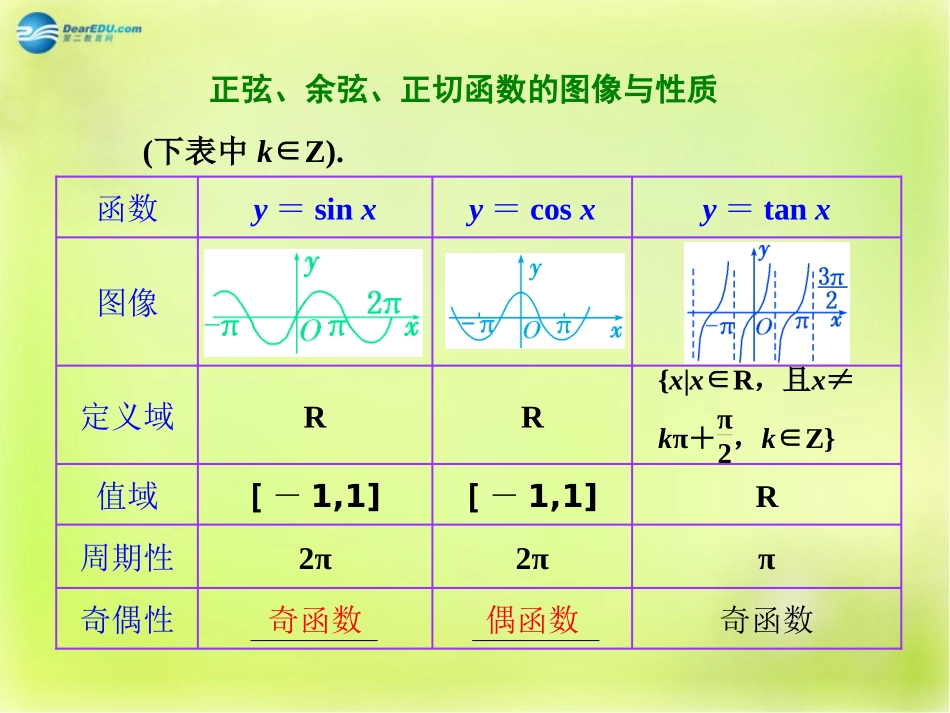
第三节三角函数图像与性质正弦、余弦、正切函数的图像与性质(下表中k∈Z).奇函数偶函数奇函数奇偶性π2π2π周期性R[－1,1][－1,1]值域RR定义域图像y＝tanxy＝cosxy＝sinx函数{x|x∈R，且x≠kπ＋π2，k∈Z}单调性y＝tanxy＝cosxy＝sinx函数2kπ－π2，2kπ＋π2为增；2kπ＋π2，2kπ＋3π2为减[2kπ，2kπ＋π]为减；[2kπ－π，2kπ]为增kπ－π2，kπ＋π2为增对称中心(kπ，0)kπ＋π2，0kπ2，0单调性y＝tanxy＝cosxy＝sinx函数2kπ－π2，2kπ＋π2为增；2kπ＋π2，2kπ＋3π2为减[2kπ，2kπ＋π]为减；[2kπ－π，2kπ]为增kπ－π2，kπ＋π2为增对称中心(kπ，0)kπ＋π2，0kπ2，0对称轴y＝tanxy＝cosxy＝sinx函数x＝kπ＋π2x＝kπ无1．三角函数存在多个单调区间时易错用“∪”联结．2．研究三角函数单调性、对称中心、奇偶性及对称轴时易忽视“k∈Z”这一条件．考点一三角函数方程三角函数不等式三角函数的定义域与值域的求法1、解三角函数方程21sin)1(x23)32cos()2(x12tan)4(x]2,0[,21)32sin()3(xx4．函数y＝tan2x＋π4的图像与x轴交点的坐标是________．解析：由2x＋π4＝kπ(k∈Z)得，x＝kπ2－π8(k∈Z)．∴函数y＝tan2x＋π4的图像与x轴交点的坐标是kπ2－π8，0.答案：kπ2－π8，02、解三角函数不等式0sin1x）（32tan2x）（21cos)3(21)4sin(4x）（的一个取值区间是（）成立的、使xxxcossin2]4,43.[A]2,2.[B]43,4.[C],0.[DA1．函数y＝tanπ4－x的定义域是()A.xx≠π4，x∈RB.xx≠－π4，x∈RC.xx≠kπ－3π4，k∈Z，x∈RD.xx≠kπ＋3π4，k∈Z，x∈R答案：D3、求三角函数定义域和值域、最值2．(2014·湛江调研)函数y＝lg(sinx)＋cosx－12的定义域为________．解析：要使函数有意义必须有sinx>0，cosx－12≥0，即sinx>0，cosx≥12，解得2kπ