高中数学 椭圆的简单几何性质教学课件 新人教A版必修5 课件VIP免费

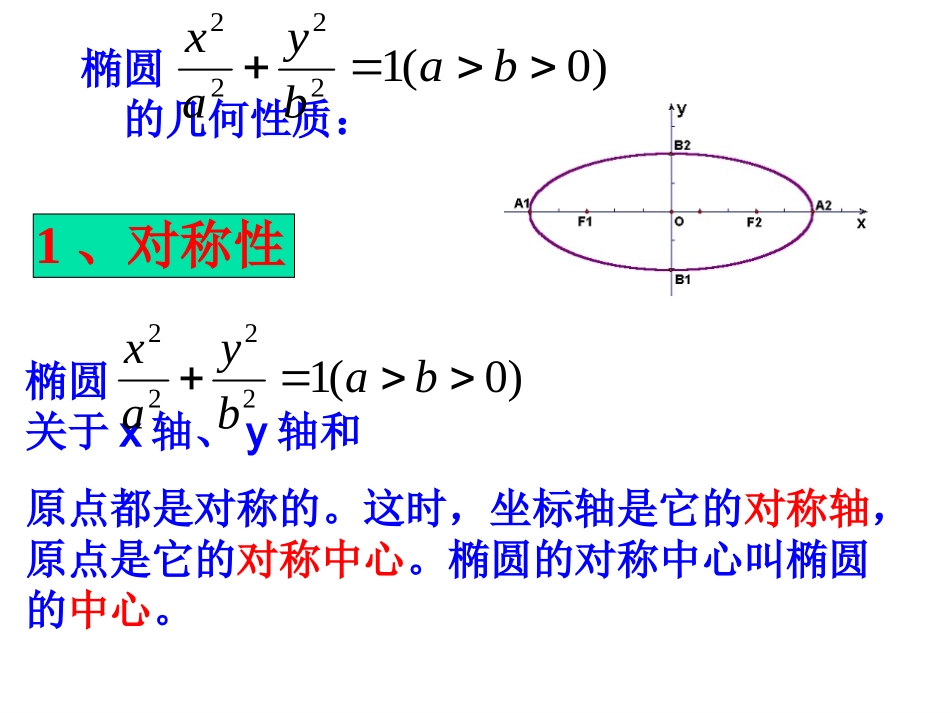
§2.1.2椭圆的简单几何性质1、椭圆的标准方程：，1)1(2222byax；1)2(2222aybx(a>b>0)222cba2、a,b,c三者的关系：椭圆的几何性质：)0(12222babyax椭圆关于x轴、y轴和原点都是对称的。这时，坐标轴是它的对称轴，原点是它的对称中心。椭圆的对称中心叫椭圆的中心。)0(12222babyax1、对称性顶点坐标:A1(-a,0)、A2(a,0)、B1(0,-b)、B2(0,b).(1)顶点：椭圆与其对称轴的交点叫做椭圆的顶点。(2)几个概念：线段A1A2、B1B2分别叫做椭圆的长轴和短轴,其中:长轴长为2a,短轴长为2ba、b分别叫椭圆的长半轴长和短半轴长。椭圆的几何性质：)0(12222babyax2、顶点椭圆的几何性质：)0(12222babyax(2)椭圆位于直线x=±a和y=±b所围成的矩形区域里。(1)-a≤x≤a,-b≤y≤b.3、范围1425(1)22yx练习1.画一画：在同一坐标系下作出下列椭圆的草图22212516()yx草图(-a,0)(a,0)(0,b)(0,-b)F2A1A2OF1xyB2B1123-1-2-3-44y123-1-2-3-44y12345-1-5-2-3-4x12345-1-5-2-3-4x1162522yx142522yx（1）（2）A1B1A2B2B2A2B1A1根据椭圆的对称性画草图椭圆的几何性质：)0(12222babyaxe越大，椭圆越扁；e越小，椭圆越圆。(1)离心率的定义：椭圆的焦距与长轴长的比e=叫做椭圆的离心率。ac(2)离心率的范围：(3)离心率对椭圆形状的影响：0b>0)离心率顶点对称性范围方程192522yx-5≤x≤5-3≤y≤3原点都是对称的关于x轴、y轴和A1(-5,0)、A2(5,0)B1(0,-3)、B2(0,3)54eaceA1(0,-a)、A2(0,a)B1(-b,0)、B2(b,0)原点都是对称的关于x轴、y轴和-a≤y≤a-b≤x≤b12222aybx小结2.求椭圆16x2+25y2=400的长轴和短轴的长、离心率、焦点和顶点坐标。解：把已知方程化成标准方程1452222yx所以，31625,4,5cba因此，椭圆的长轴长和短轴长分别是82,102ba离心率6.053ace焦点坐标分别是)0,3(),0,3(21FF四个顶点坐标是)4,0(),4,0(),0,5(),0,5(2121BBAA3、若焦点在x轴上的椭圆的离心率为，则m为（）。A、B、C、D、4、下列方程所表示的曲线中，关于x轴、y轴都对称的是（）。A、B、C、D、5、方程（a＞b＞0,k＞0且k≠1)与方程（a＞b＞0)表示的椭圆（）。A、有等长的短轴、长轴；B、有共同的交点；C、有相同的离心率；D、有相同的顶点。1222myx213233832yx42022yxyxxyx54224922yx12222kbykax12222byaxBDC例1．求适合下列条件的椭圆的标准方程：长轴长等于,离心率等于．2035例2.已知椭圆的中心在原点，焦点在坐标轴上，长轴是短轴的三倍，且椭圆经过点P（3，0），求椭圆的方程。创新提高：0).(k22kkyx2、椭圆的长轴是短轴的2倍，则k=____.1、如果一椭圆短轴上的一个顶点与两个焦点构成一个正三角形，求椭圆的离心率。小结小结：离心率顶点对称性范围椭圆方程12222byax12222bxay椭圆的性质：-a≤x≤a-b≤y≤b原点都是对称的关于x轴、y轴和A1(-a,0)、A2(a,0)B1(0,-b)、B2(0,b)aceaceA1(0,-a)、A2(0,a)B1(-b,0)、B2(b,0)原点都是对称的关于x轴、y轴和-a≤y≤a-b≤x≤b小结2作业：