高中数学(空间向量及其运算三)课件 新人教版选修2-1 课件VIP免费

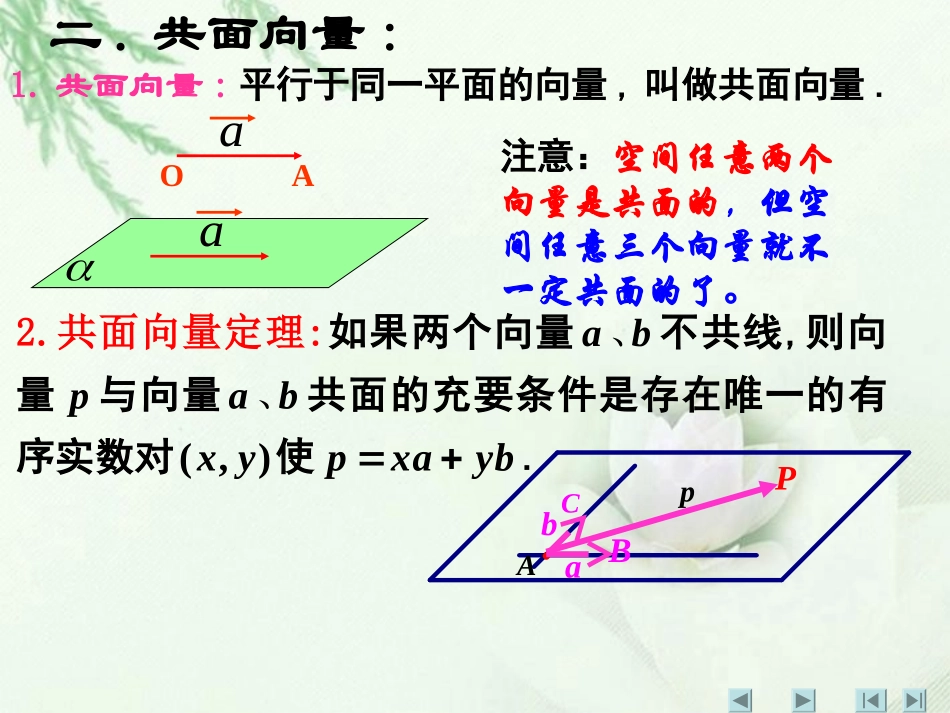
复习回顾:一、共线向量1.共线向量:如果表示空间向量的有向线段所在的直线互相平行或重合，则这些向量叫做共线向量或平行向量．a平行于b记作//ab．规定:o与任一向量a是共线向量.2.共线向量定理：空间任意两个向量a、b（b≠0），a//b的充要条件是存在实数，使ab.共线与共面分析lAPa注:非零向量a叫做直线l的方向向量.二.共面向量:1.共面向量:平行于同一平面的向量,叫做共面向量.OAaa注意：空间任意两个向量是共面的，但空间任意三个向量就不一定共面的了。2.共面向量定理:如果两个向量ab、不共线,则向量p�与向量ab、共面的充要条件是存在唯一的有序实数对(,)xy使pxayb�.AabBCPp�三、平面向量基本定理：平面向量的正交分解及坐标表示xyoaijaxiyj(1,0),(0,1),0(0,0).ijyxa,问题：我们知道，平面内的任意一个向量都可以用两个不共线的向量来表示（平面向量基本定理）.对于空间任意一个向量，有没有类似的结论呢？,abp�一、空间向量基本定理：都叫做基向量,,abc{,,}.abc��叫做空间的一个基底注:如果三个向量不共面,那么对空间任一向量,存在有序实数组{x,y,z}使,,abcP�.pxaybzc�（1）任意不共面的三个向量都可做为空间的一个基底.特别提示：（2）由于可视为与任意一个非零向量共线,与任意两个非零向量共面,所以三个向量不共面,就隐含着它们都不是.00（3）一个基底是指一个向量组,一个基向量是指基底中的某一个向量,二者是相关连的不同概念.二、空间直角坐标系单位正交基底：一个基底的三个基向量互相垂直，且长都为1，则这个基底叫做单位正交基底。常用e1,e2,e3表示空间直角坐标系：在空间选定一点O和一个单位正交基底e1,e2,e3,以点O为原点，分别以e1,e2,e3的方向为x轴、y轴、z轴的正方向，建立一个空间直角坐标系O--xyzxyze1e2e3O121323112233,,,,,.eeeeeeeeeeee��计算单位正交基之间的数量积在空间直角坐标系O–xyz中，对空间任一点P,对应一个向量,于是存在唯一的有序实数组x,y,z,使(如图).OP�123OPxeyeze�xyzOP(x,y,z)即(,,)(,,)OPxyzPxyz�点P的坐标为(x,y,z),记作P(x,y,z)，其中x叫做点P的横坐标,y叫做点P的纵坐标,z叫做点P的竖坐标.e1e2e3一个向量在直角坐标系中的坐标等于一个向量在直角坐标系中的坐标等于表示这个向量的有向线段的终点的坐标减去表示这个向量的有向线段的终点的坐标减去起点的坐标起点的坐标..AB=OB-OA=(x2,,y2,z2)-(x1,y1,z1)=(x2-x1,y2-y1,z2-z1).思考：设A(x1,y1,z1),B(x2,y2,z2),则AB的坐标表示是什么？则1122(,)abab))(,(21Raaababa//ab三、平面向量的坐标运算（一）12121122(,),(,),(,),(,)aaabbbAxyBxy设121122112221,,,0aaaabababbbb即2121(,)ABOBOAxxyy�设M=（x，y），若M是线段AB的中点，1212xxyy,22xy则133122(,,)abababab123(,,)()aaaaRab//ab三、空间向量的坐标运算（一）设121122331233,,,aaababbbaabb即121122(,,)ABOBOAxxyyzz�设M=（x，y，z），若M是线段AB的中点，123231231+xxyyxyzz,z2,22zxy331121211222(,,),(,,),(,,),(,,)abzaaabbbAxyBxyz四、平面向量的距离与夹角1.距离公式12121122(,),(,),(,),(,)aaabbbAxyBxy设则2212||aaaaa222121||()()�ABABABxxyy问：此公式有何几何意义。2.夹角公式112222221212cos,||||abababababaabb01122,90cos,000abababababab四、空间向量的距离与夹角1.距离公式133212112122(,,),(,,),(,,),(,,)aaabbbAxayzBbzyx设212232||aaaaaa222121221||()()()�ABABABxzzxyy问：此公式有何几何意义。2.夹角公式112222221212332233cos,||||ababababababa...