高中数学 222 向量减法运算及其几何意义4课件 新人教A版必修4 课件VIP免费

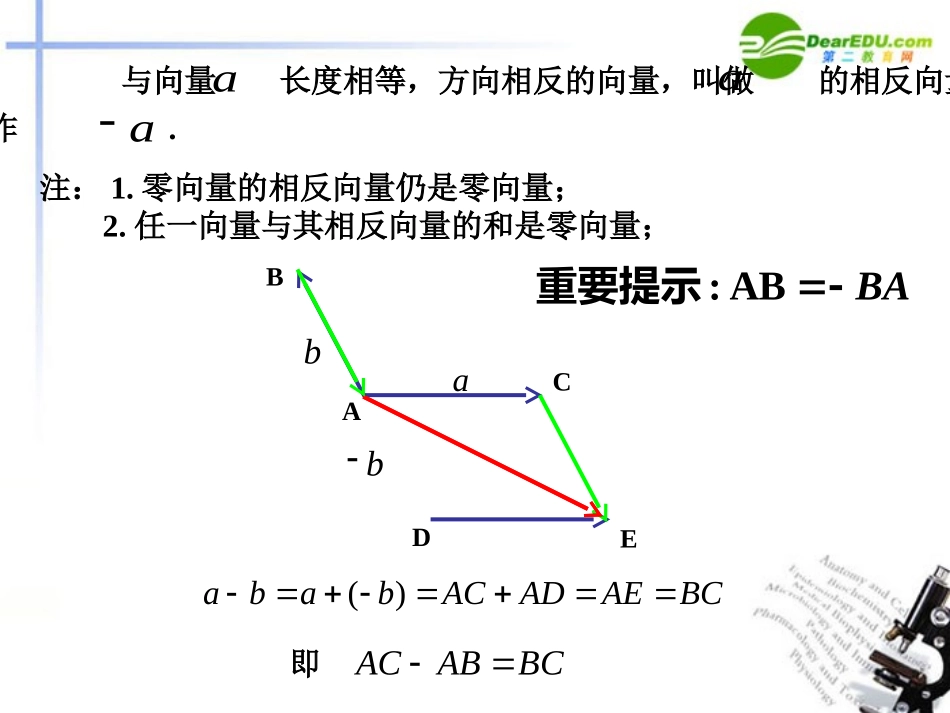
向量的减法看书P94~96（限时5分钟）学习目标：通过实例，掌握向量的减法运算及理解其几何意义。熟练运用减法的“三角形法则”并与加法法则作比较.练习：判断下列命题是否正确。①如果模不相等的非零向量与的方向相同或相反，那么的方向必与其中之一的方向相同；abab,ab②△ABC中，必有；0ABBCCA�③若，则A、B、C为一个三角形的三个顶点；0ABBCCA�④若均为非零向量，则与一定相等.,ab||ab||||ab温故知新(1分钟)与向量长度相等，方向相反的向量，叫做的相反向量，记作.aaa注：1.零向量的相反向量仍是零向量；2.任一向量与其相反向量的和是零向量；ABCabDbE()ababACADAEBC��ACABBC�即:ABBA重要提示�abOBAabab向量的减法：,,,,abOOAaOBbBAabababOAOBBA�����、内点，则与，记这减则已知向量在平面任取一作向量叫做的差作即种求向量差的方法，叫做向量法的三角形法。起点相同指向被减向量abab、线则应样：若向量共，怎作出呢？思考abab（1）（2）OABABOabab||||||||||||||||ababababababba若，方向相反，若，方向相同，（或）||||||ababab若，不共线，则||||||||||abababab对任意两个向量，，有||.,,,,,.1dcbadcba求作向量已知向量例ababccddABCDO.,,,.2.,,,,.1:为所求则作作在平面上任取点作法dcDCbaBADCBAdODcOCbOBaOAO限时训练（3分钟）P96练习1、2、3DBACbabADaABABCD,,,,,.2表示向量用已知平行四边形例abABCD解：有向量加法的平行四边形法则，得ACab�;由向量的减法可得，.DBABADab�练习.化简：()()ABCDACBD�:ABBA重要提示�课后练习:P101习题4、5