高中数学(空间向量及其运算)课件 新人教版选修2-1 课件VIP免费

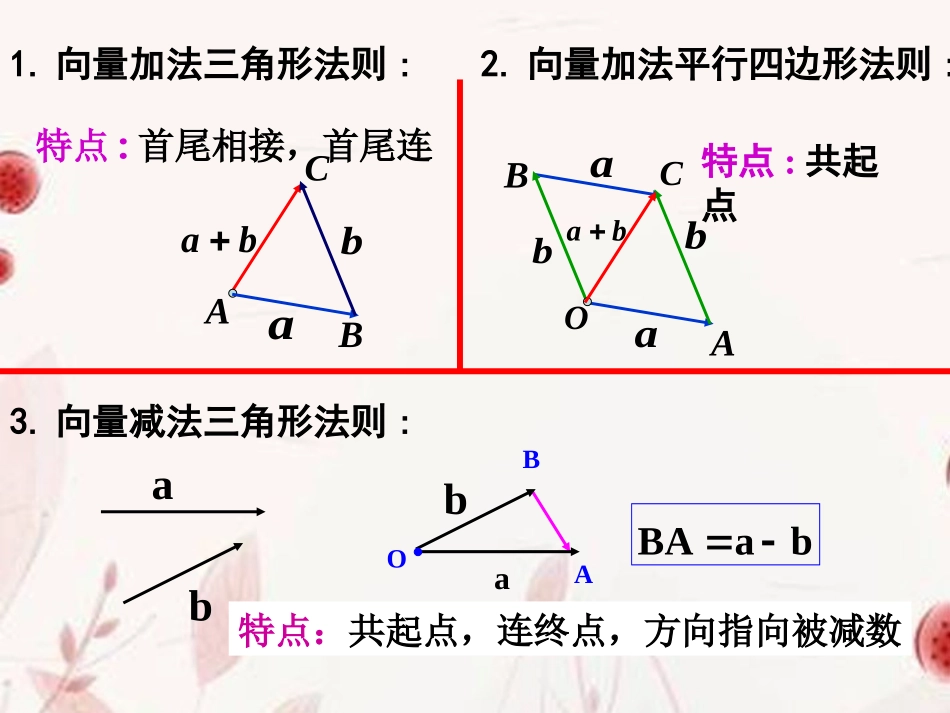
向量：既有大小又有方向的量AB�AB向量aABa零向量：长度为0的向量，记为；单位向量：长度为1的向量.01.定义2.表示方法3.模（大小）4.其它向量相等向量：相反向量：方向相同或相反的非零向量叫平行向量.平行向量（共线向量）：二．温故知新二．温故知新1.向量加法三角形法则:aAbBCbaaaAbBbOCba特点:首尾相接，首尾连特点:共起点babBaABAab�O特点：共起点，连终点，方向指向被减数2.向量加法平行四边形法则:3.向量减法三角形法则:)()(cbacbaabba加法交换律加法结合律4.运算律:凡涉及空间两个向量的问题，平面向量中有关结论仍适用于它们。空间向量加法的推广:（1）首尾相接的若干向量之和，等于由起始向量的起点指向末尾向量的终点的向量；nnAAAAAAAA1433221（2）首尾相接的若干向量若构成一个封闭图形，则它们的和为零向量.1433221AAAAAAAAnnAA10化简结果的向量：列向量表达式，并标出，化简下已知平行六面体''''DCBAABCD；⑴BCAB；⑵'AAADAB．)'(31)3(AAADABABCDA’B’C’D’例1.；⑴BCAB解：ABCDA’B’C’D’BCAB⑴AC；⑵'AAADAB'AAADAB⑵'AAAC'CCAC'AC结论：始点相同的三个不共面的向量之和，等于以这三个向量为棱的平行六面体的公共始点为始点的对角线所示向量。——平行六面体法则)'(31AAADAB设G是线段AC’靠近点A的三等分点，则G.．)'(31)3(AAADABABCDA’B’C’D’'31AC．AG设M是线段CC’的中点，则解：'21CCADABCMACAMABCDA’B’C’D’M''''1'2ABCDABCDABADCC�练习1.已知平行六面体，化简，并标出化简结果的向量：解：ABCDA’B’C’D’M'''''''ABCDABCDABADAABDBC�练习2.已知平行六面体，用，，，表示向量和''BDBABCBB�'ABADAA�''BCBBBC�'AAAD�平面向量概念加、减法运算运算律定义表示法相等向量减法:三角形法则加法:平行四边形法则或三角形法则空间向量)()(cbacbaabba加法交换律加法结合律小结类比方法数形结合思想零向量相反向量减法:三角形法则加法:平行四边形法则或三角形法则不共面的三个向量的和：平行六面体法则aa实数与空间向量的乘积仍然是一个向量.1.空间向量的数乘运算（1）大小：|λa|＝|λ|·|a|;（2）方向：λ＞0时同向，λ＜0时反向，λ＝0时λa＝0.1.空间向量的数乘运算（3）运算律：分配律：（a+b）=a+b结合律：（a）=a2.共线向量,(0),//.bbabab共线向量基本定理：对空间任意两个向量a存在实数，使得lAPa存在实数t，使APta=uuurr点P在直线l上ÛOOPOAtaÛ=+uuuruuurrBOPOAtABÛ=+uuuruuuruuur()OPOAtOBOAÛ=+-uuuruuuruuuruuur(1)OPtOAtOBÛ=-+uuuruuuruuur若，则点P、A、B共线的充要条件是x＋y＝1；OPxOAyOB=+uuuruuuruuur3.共面向量平行于同一平面的向量，叫做共面向量空间任意两个向量是共面的，但空间任意三个向量就不一定共面。3.共面向量若向量a，b不共线，则向量p与a，b共面的充要条件是：存在惟一的有序实数对(x，y)，使p＝xa＋yb.AabBCp��p存在有序实数对(x，y)，使空间一点P位于平面ABC内APBCAPxAByAC=+uuuruuuruuurÛOOPOAxAByACÛ-=+uuuruuuruuuruuur()()OPOAxOBOAyOCOAÛ-=-+-uuuruuuruuuruuuruuuruuur(1)OPxyOAxOByOCÛ=--++uuuruuuruuuruuur对空间任一点O和不共线三点A、B、C，若，则点P在平面ABC内的充要条件是x＋y＋z＝1.OPxOAyOBzOC=++uuuruuuruuuruuur则x+y+z=1是四点P、A、B、C共面的（）1.若对任一点O和不共线的三点A、B、C，且有),,,(RzyxOCzOByOAxOPA.必要不充分条件C.充要条件B.充分不必要条件D.既不充分也不必要条件COAOPOCOB3)1(2.已知A、B、C三点不共线，对于平面ABC外的任一点O，确定在下列各条件下，点P是否与A、B、C一定共面？OCOBOAOP4)2(例2.如图，已知平行四边形ABCD，过平面AC外一点O作射线OA、OB、OC、OD，在四条射线上分别取点E、F、G、H，并且使求证：四点E、F、G、H共面；,OEOFOGOHkOAOBOCODOBAHGFECD共线向...