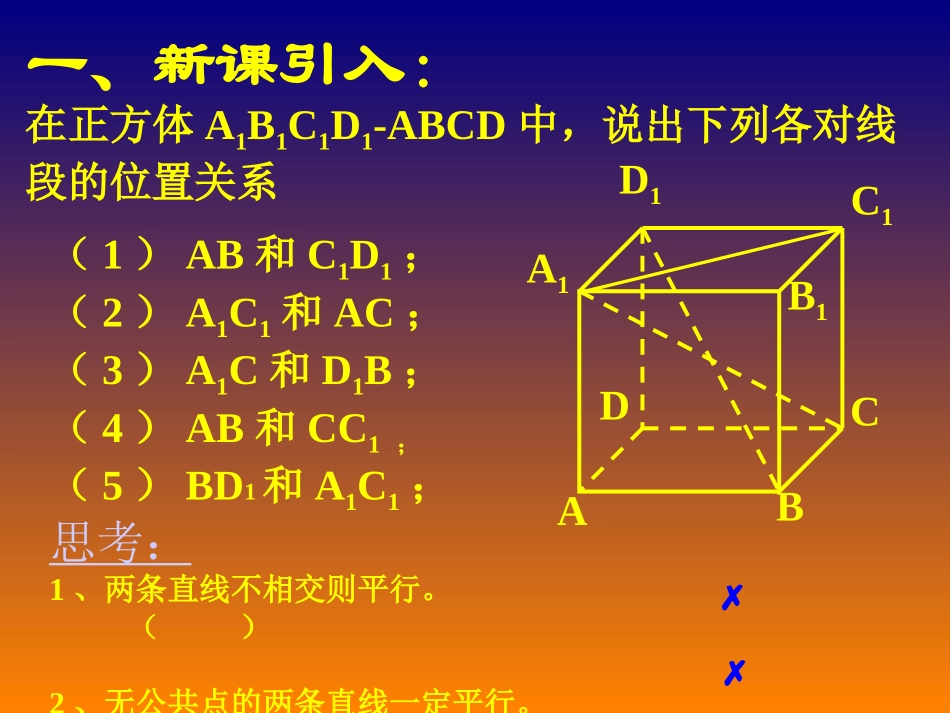
直线与直线的位置关系(2)一、新课引入:在正方体A1B1C1D1-ABCD中,说出下列各对线段的位置关系(1)AB和C1D1;(2)A1C1和AC;(3)A1C和D1B;(4)AB和CC1;(5)BD1和A1C1;思考:1、两条直线不相交则平行。()2、无公共点的两条直线一定平行。()ABCDA1B1C1D1二、新授:两条不重合直线之间有、lmPml图1图2llll(一)、空间中两直线的位置关系从图中可见,直线l与m既不相交,也不平行。空间中直线之间的这种关系称为异面直线。在空间中,相交平行及异面直线三种位置关系.(1)从公共点的数目来看可分为:①有且只有一个公共点则两直线相交两平行直线②没有公共点则两直线为异面直线(2)从平面的性质来讲,可分为:两直线相交①在同一平面内两直线平行②不同在任何一个平面内则两直线为异面直线。定义:不同在任何一个平面内不同在任何一个平面内的两条直线为异面直线(一)、空间中两直线的位置关系:1、空间中两直线的位置关系分类:2.判定异面直线的方法:(1)根据异面直线的定义:应用反证法来证明。3.异面直线的画法:(2)过平面内一点与平面外一点的直线,和这个平面内不经过该点的直线是异面直线。(可作判断依据)是异面直线与直线,,若用符号表示为llBBlAlAB,Abaαbaba两条都是平行直线,但是它们之间有什么区别?“定量”研究平行线,必须引入“距离”的概念问题回顾:abca与b是相交直线,a与c也是相交直线,它们之间又有什么区别?“定量”研究相交直线,必须引入“角”的概念NaMbcd直线a与b,直线a与c,直线a与d都是异面直线,它们有什么区别?直线a与b,直线a与c,都是异面直线,它们有什么区别?aMbc异面直线所成的角的定义aMba1b1直线a,b是异面直线,经过空间任意一点o,分别引直线a1∥a,b1∥b,我们把直线a1和b1所成的锐角(或直角)叫做异面直线a和b所成的角。o.a1a1a1a1a1a1a1a1a1a1a1a1a1a1a1a1a1a1a1a1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1b1aMba1b1o.a2b2o1.O是空间中的任意一点所成的锐角是否相等?点o常取在两条异面直线中的一条上aMbo点o常取在两条异面直线中的一条上相交直线所成角的大小,就是异面直线所成角的大小相交直线a,b所成的角?异面直线所成的角?异面直线所成的角的范围?00°﹤90°≤(二)、异面直线所成角的定义:1.直线a、b是异面直线。经过空间任意一点O,分别引直线a1a∥,b1b∥。我们把直线a1和b1所成的锐角(或直角)叫做异面直线a和b所成的角。aαa1b1ObaαOθ为了简便,点O常取在两条异面直线中的一条上。o9002.异面直线a和b所成的角的范围:abOa1b1Oab1b3.找角方法:β如果两条异面直线所成的角是直角,就说这两条异面直线互相垂直。相交垂直(有垂足)垂直异面垂直(无垂足)OααO因此,异面直线所成角的范围是(0,]4、特例:2例1.如图,在正方体中,(1)哪些棱所在的直线与直线BA1成异面直线?(2)求直线BA1和CC1所成的角的大小。ABCDA1B1C1D1(三)、例题分析:解:(2) BB//CC,且BB∩BA=B1111∴∠ABB为异面直线AB与CC所成角的平面角.1111∴异面直线BA与CC所成的角为45011又 ∠ABB=45011求求异面直线所成的角的一般步骤的一般步骤是是::根据异面直线所成角的定义,求异面直线所成角,就是要将其变换成相交直线所成有角。其一般方法有:(1)平移法:即根据定义,以“运动”的观点,用“平移转化”的方法,使之成为相交直线所成的角。(1)(1)找出或作出有关的图形;找出或作出有关的图形;(2)(2)证明它符合定义;证明它符合定义;(3)(3)计算。计算。[[即:要求先证,要证先即:要求先证,要证先作。作。]]具体地讲是选择“特殊点”作异面直线的平行线,具体地讲是选择“特殊点”作异面直线的平行线,构作含异面直线所成的角构作含异面直线所成的角((或其补角或其补角))的三角形,再求的三角形,再求之。之。例例2::长方体ABCD-A1B1C1D1,AB2cm,AD1cm,求异面直线A1C1与BD1所成的角。O1M(2)补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体等,其目的在于易于发现两条异面直线的关系。BDB1A1D1C1ACF1...