高中数学 正弦函数的图象和性质课件 新人教B版必修4 课件VIP免费

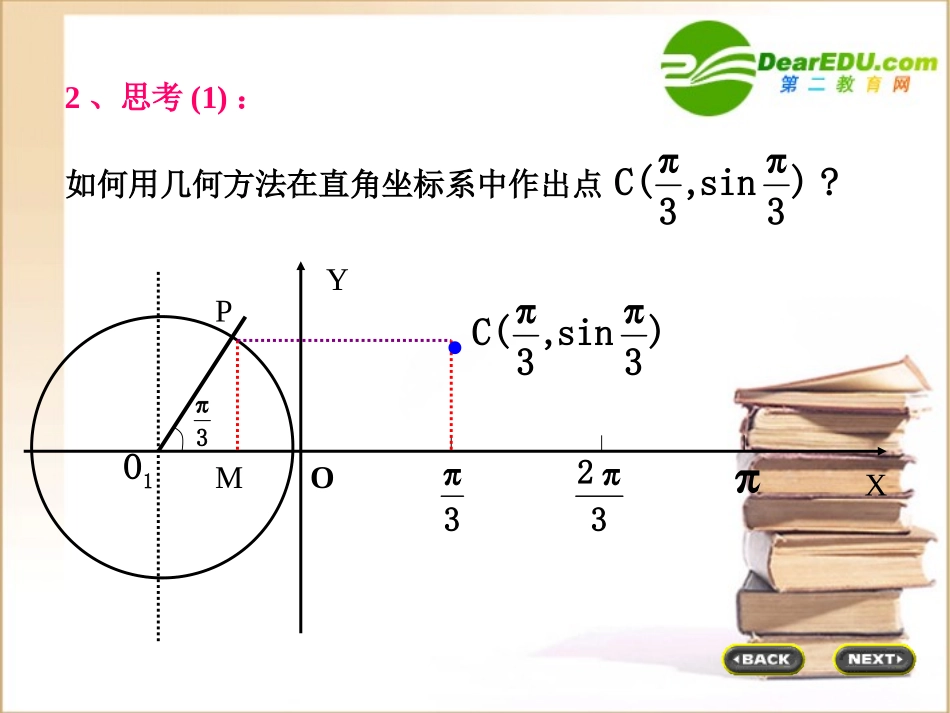
高一数学组(1)列表(2)描点(3)连线1.用描点法作出函数图象的主要步骤是什么？2、思考(1)：?)3πsin,3πC(如何用几何方法在直角坐标系中作出点OP1O3πMXY3π32ππ)3πsin,3πC(.思考(2):能否借助上面作点C的方法，在直角坐标系中作出正弦函数Rxsinx,y的图象呢？作正弦函数的图象o1xyy=sinx,x[0,2]o2322667236113653435-11作正弦函数的图象y=sinx,x[0,2]o1o1xy2322667236113653435-1作正弦函数的图象y=sinx,x[0,2]o1o1xy2322667236113653435-1y=sinxx[0,2]y=sinxxR终边相同角的三角函数值相等即：sin(x+2k)=sinx,kZ)()2(xfkxf利用图象平移x6yo--12345-2-3-41正弦曲线与x轴的交点)0,0()0,()0,2(图象的最高点图象的最低点)1,(23(五点作图法)2oxy---11--13232656734233561126)1,2(简图作法(1)列表(列出对图象形状起关键作用的五点坐标)(3)连线(用光滑的曲线顺次连结五个点)(2)描点(定出五个关键点)列表(2)描点作图（1）y=2sinx,x∈[0,2π]解:（1）例1.分别作出下列函数简图（五点法作图）x02223020-20Y2X02y=2sinxy=2sinx1y=sinx列表(2)描点作图（2）y=sin2x,x∈[0,π]解:（1）2、五点作图法x022232x010-1004432Y1X0y=sin2x2y=sin2xy=sinx_____maxy_____miny（3）周期性当x=________________时，当x=________________时，值域是：（2）值域（1）定义域xOy11223222341y1y正弦函数y=sinx的性质：R实数集Zkk,221111，2TZkk,22(5)单调性(6)奇偶性是______函数，图象关于_______对称为增函数，内，在_____________________xRx为减函数______________________x奇原点(4)最大值与最小值_____maxy_____miny11Zkkk,22,22Zkkk,232,22xOy11223222341y1y正弦函数y=sinx的性质：例2求y=5+sinx这个函数的最大值、最小值和周期，并求这个函数分别取得最大值及最小值的x的集合。使y=5+sinx取得最大值的x的集合是:Zkkxx,22使y=5+sinx取得最小值的x的集合是:Zkkxx,22615maxy415miny2T解：小结：1、用单位圆中的正弦线画出正弦函数的图象。2、利用五点法作正弦函数的简图。3、观察图象得出正弦函数的性质作业：成才之路