高中数学(空间中的距离问题)课件 新人教版选修2-1 课件VIP免费

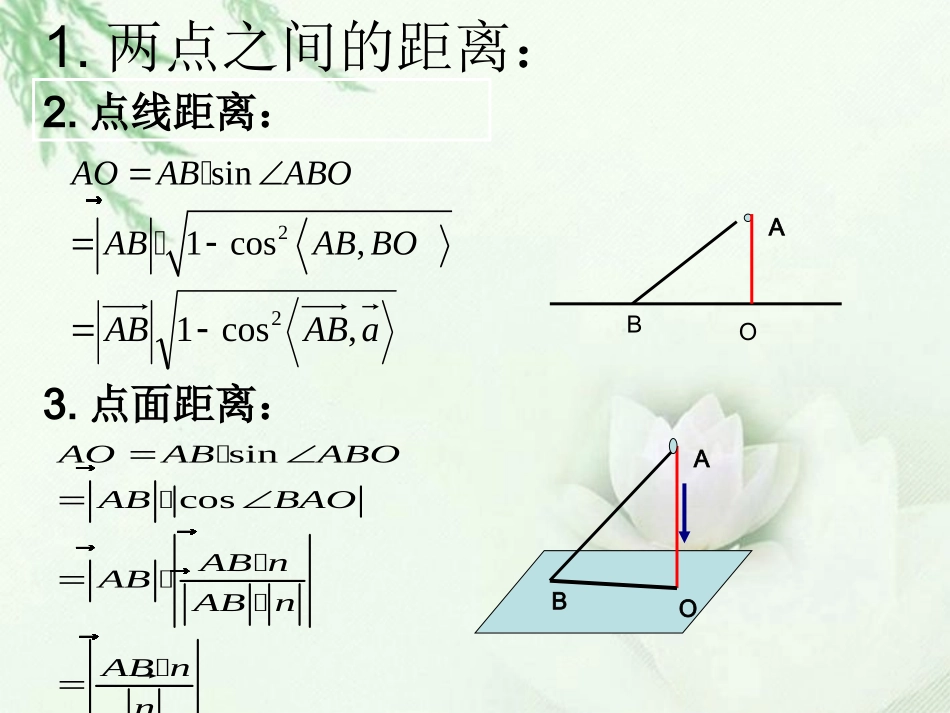
复习回顾：夹角计算公式(1)线线角：直线与直线所成的角为θ，如两直线的方向向量分别为a，b，则cosθ＝|cos〈a，b〉|；(2)线面角：直线与平面所成的角为θ，如直线的方向向量为a，平面的法向量为n，则sinθ＝|cos〈a，n〉|；(3)面面角：两相交平面所成的角为θ，两平面的法向量分别为n1和n2，则cosθ＝|cos〈n1，n2〉|，其特殊情况是两个半平面所成的角即二面角，也可以用这个公式解决，但要判定二面角的平面角是锐角还是钝角的情况以决定cosθ＝|cos〈n1，n2〉|还是cosθ＝－|cos〈n1，n2〉|.1.两点之间的距离：2sin1cos,AOABABOABABBO�sincosAOABABOABBAOABnABABnABnn�����2.点线距离：ABO3.点面距离：ABOaABAB,cos124.线面距离：nnABdA5.面面距离A转化为点面距离转化为点面距离nnABd•如图所示，在平行四边形ABCD中，AB＝AC＝1，∠ACD＝90°，将它沿对角线AC折起，使AB与CD成60°角，求B、D间的距离．[规范作答]∵∠ACD＝90°，∴AC→·CD→＝0.同理AC→·BA→＝0.∵AB与CD成60°角，∴〈BA→，CD→〉＝60°或120°.又BD→＝BA→＋AC→＋CD→，∴BD→·BD→＝|BA→|2＋|AC→|2＋|CD→|2＋2BA→·AC→＋2BA→·CD→＋2AC→·CD→＝3＋2×1×1×cos〈BA→，CD→〉当〈BA→，CD→〉＝60°时，BD→2＝4，|BD→|＝2，当〈BA→，CD→〉＝120°时，BD2＝2，|BD→|＝2.10分∴B、D两点间的距离为2或2.12分•[题后感悟]求空间中两点间距离的主要方法•(1)建立空间直角坐标系，求出两点的坐标，代入两点间距离公式求解；•(2)将以两点为端点的向量用基向量表示，再求此向量•例2．已知正方形ABCD的边长为1，PD⊥平面ABCD，且PD＝1，E，F分别为AB，BC的中点．•(1)求点D到平面PEF的距离；•(2)求直线AC到平面PEF的距离．•解析：•(1)建立以D为坐标原点，DA，DC，DP分别为x轴，y轴，z轴的空间直角坐标系，如图所示．则P(0,0,1)，A(1,0,0)，C(0,1,0)，E1，12，0，F12，1，0，EF→＝－12，12，0，PE→＝1，12，－1，设平面PEF的法向量n＝(x，y，z)，则n·EF→＝0，且n·PE→＝0，所以02102121zyxyx令x＝2，则y＝2，z＝3，所以n＝(2,2,3)，所以点D到平面PEF的距离为d＝|DE→·n||n|＝|2＋1|4＋4＋9＝31717，因此，点D到平面PEF的距离为31717.(2)因为AE→＝0，12，0，所以点A到平面PEF的距离为d＝|AE→·n||n|＝117＝1717，所以AC到平面PEF的距离为1717.拓展提高：如图，已知ABCD是矩形，AB=a,AD=b,PA⊥平面ABCD，PA=2c,Q是PA的中点求(1)Q到BD的距离；(2)P到平面BQD的距离HEQPDCBA新疆王新敞特级教师源源源源源源http://www.xjktyg.com/wxc/wxckt@126.comwxckt@126.comhttp://www.xjktyg.com/wxc/源源源源源源特级教师王新敞新疆22baab2122222babac22222babac新疆源头学子小屋特级教师王新敞http://www.xjktyg.com/wxc/wxckt@126.comwxckt@126.comhttp://www.xjktyg.com/wxc/王新敞特级教师源头学子小屋新疆HEQPDCBA解(1)在矩形ABCD中，作AE⊥BD，E为垂足连结QE，∵QA⊥平面ABCD，由三垂线定理得QE⊥BE∴QE的长为Q到BD的距离在矩形ABCD中，AB=a,AD=b,∴AE=在Rt△QAE中，QA=PA=c∴QE=∴Q到BD距离为新疆王新敞特级教师源源源源源源http://www.xjktyg.com/wxc/wxckt@126.comwxckt@126.comhttp://www.xjktyg.com/wxc/源源源源源源特级教师王新敞新疆新疆源头学子小屋特级教师王新敞http://www.xjktyg.com/wxc/wxckt@126.comwxckt@126.comhttp://www.xjktyg.com/wxc/王新敞特级教师源头学子小屋新疆22baab22222)(bacbaabc(2)∵平面BQD经过线段PA的中点，∴P到平面BQD的距离等于A到平面BQD的距离在△AQE中，作AH⊥QE，H为垂足∵BD⊥AE,BD⊥QE,∴BD⊥平面AQE∴BD⊥AH∴AH⊥平面BQE，即AH为A到平面BQD的距离在Rt△AQE中，∵AQ=c,AE=∴AH=∴P到平面BD的距离为22222)(bacbaabc新疆王新敞特级教师源源源源源源http://www.xjktyg.com/wxc/wxckt@126.comwxckt@126.comhttp://www.xjktyg.com/wxc/源源源源源源特级教师王新敞新疆新疆源头学子小屋特级教师王新敞http://www.xjktyg.com/wxc/wxckt@126.comwxckt@126.comhttp://www.xjktyg.com/wxc/王新敞特级教师源头学子小屋新疆解法二设点A到平面QBD的距离为h，由VA—BQD=VQ—ABD,得31S△BQD·h=31S△ABD·AQh=22222)(bacbaabcSAQSBQDABD课堂小结：•1.求两点之间的距离：•2.求点面之间的距离：•3.求线面之间的距离：