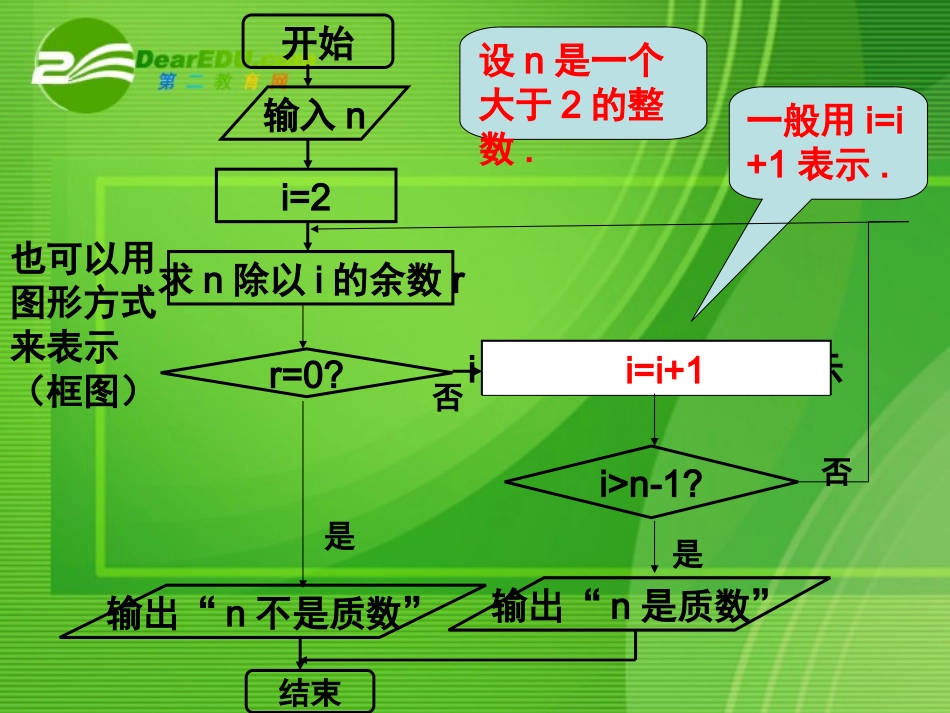
1.1.2程序框图与算法的基本逻辑结构任意给定一个大于1的整数n,试设计一个程序或步骤对n是否为质数做出判定.算法分析:从上节课我们知道:算法可以用自然语言来描述.•第一步,给定大于2的整数n•第二步,令i=2•第三步,用i除n,得到余数r•第四步,判断“r=0”是否成立,若是,则n不是质数,结束算法;否则令i=i+1•第五步,判断“i>(n-1)”是否成立,若是,则n是质数,结束算法;否则返回第三步开始输入ni=2求n除以i的余数ri的值增加1仍用i表示i>n-1?输出“n不是质数”结束是否是输出“n是质数”否r=0?设n是一个大于2的整数.一般用i=i+1表示.i=i+1也可以用图形方式来表示(框图)思考?通过上述算法的两种不同表达方式的比较,你觉得用程序框图来表达算法有哪些特点?用程序框图表示的算法更加简练,直观,流向清楚.程序框图又称流程图,是一种用程序框、流程线及文字说明来准确、直观地表示算法的图形.一个或几个程序框的组合表示算法中的一个步骤;带有方向箭头的流程线将程序框连接起来,表示算法步骤的执行顺序.基本的程序框和它们各自表示的功能如下:图形符号名称功能终端框(起止框)表示一个算法的起始和结束输入、输出框表示一个算法输入和输出的信息处理框(执行框)判断某一条件是否成立,成立时在出口处标明“是”或“Y”;不”成立时标明“否”或“N”.判断框赋值、计算流程线连接程序框连接点连接程序框图的两部分开始输入ni=2求n除以i的余数ri=i+1i>n-1或r=0?结束是否是否r=0?顺序结构用程序框图来表示算法,有三种不同的基本逻辑结构:条件结构循环结构输出“n不是质数”输出“n是质数”程序框图的三种基本的逻辑结构顺序结构条件结构循环结构(1)顺序结构-----是由若干个依次执行的处理步骤组成的.这是任何一个算法都离不开的基本结构.例1:已知一个三角形的三边边长分别为a,b,c,利用海伦-秦九韶公式设计一个算法,求出它的面积,画出算法的程序框图.()()()Sppapbpc2abcp例1:已知一个三角形的三边边长分别为a,b,c,利用海伦-秦九韶公式设计一个算法,求出它的面积,画出算法的程序框图.算法分析:第二步:计算p的值.第三步:由海伦-秦九韶公式求出三角形的面积S.第四步:输出S的值.第一步:输入三角形三条边的边长a,b,c画出:已知三角形的三边长a,b,c,求它的面积的程序框图.开始2abcp()()()Sppapbpc输出S结束输入a,b,c练习1已知两个单元分别存放了x和y的值。试交换这两个变量值。设计算法,并用框图表示(2)条件结构---在一个算法中,经常会遇到一些条件的判断,算法的流向根据条件是否成立有不同的流向.条件结构就是处理这种过程的结构.满足条件?步骤A步骤B是否满足条件?步骤A是否例2:任意给定3个正实数,设计一个算法,判断分别以这3个数为三边边长的三角形是否存在.画出这个算法的程序框图.算法分析:第一步:输入3个正实数a,b,c;第二步:判断a+b>c,a+c>b,b+c>a是否同时成立,若是,则能组成三角形;若否,则组不成三角形.程序框图:开始输入a,b,ca+b>c,a+c>b,b+c>a是否同时成立?是存在这样的三角形不存在这样的三角形否结束例3:为了加强居民的节水意识,某市制订了以下生活用水收费标准:每户每月用水未超过7m3时,每立方米收费1.0元,并加收0.2元的城市污水处理费;超过7m3的部分,每立方米收费1.5元,并加收0.4元的城市污水处理费,请你写出某户居民每月应交纳的水费y(元)与用水量x(m3)之间的函数关系,然后设计一个求该函数值的算法,并画出程序框图.解:y与x之间的函数关系为:1.2,1.94.9xyx(当0≤x≤7时)(当x>7时)解:y与x之间的函数关系为:1.2,1.94.9xyx(当0≤x≤7时)(当x>7时)算法分析:第一步:输入每月用水量x;第二步:判断x是否不超过7.若是,则y=1.2x;若否,则y=1.9x-4.9.第三步:输出应交纳的水费y.开始输入用水量x0≤x≤7?是y=1.2x否y=1.9x-4.9输出y结束程序框图例4.画程序框图,对于输入的x值,输出相应的y值.0(0)1(01)(1)xyxxx开始程序框图x<0?是y=0否0≤x<1?是y=1否y=x输出y结束输入x是练习2.设计一个求任意数的绝对值的算法,并画出程序框图.(0)||(xxxxx当时当<0时)算法分析:第一步:输入数x;第二步:判断x≥0是否成立?...