高中数学 113(导数的几何意义)课件 新人教B版选修2-2 课件VIP免费

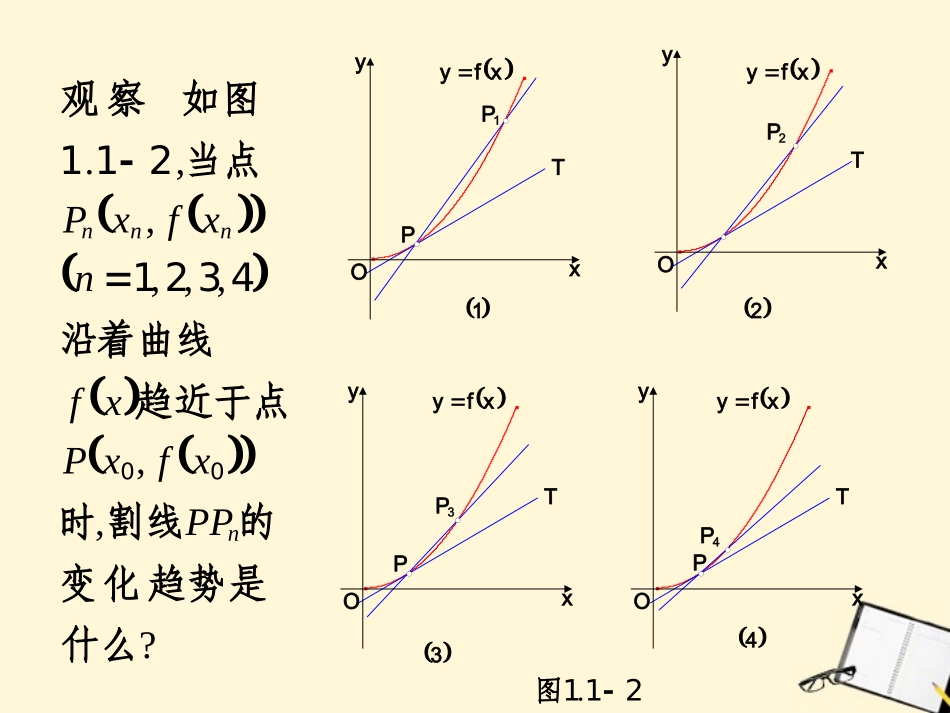
导数的几何意义311..?,.,,''的几何意义是什么呢导数么那附近的变化情况在数反映了函处的瞬时变化率在表示函数导数我们知道0000xfxxxfxxxfxfP1P2P3P4PTTTTPPxfyxfyxfyxfyOyxOyxOyxOyx211.图1234?,,,,,,,.什么是趋势化变的割线时趋近于点沿着曲线当点图如察观nnnnPPxfxPxfnxfxP004321211?,.tan,,,有什么关系呢的斜率斜率与切线的割线值得关注的问题是的称为过点这个确定位置的直线定的位置趋近于确割线时趋近于点当点我们发现kPTPPlinegentPPTPPPPnnn切线?同过的切线定义有什么不此处切线定义与以前学.,00xxxfxfkPPnnnn的斜率是割线容易知道.lim.,.,'00000xfxxfxxfkkPTxxxfPTkPPxnn即的斜率线处的导数就是切在函数因此的斜率无限趋近于切线时无限趋近于点当点.,,,...,.附近的变化情况在述、比较曲线请描据图象根图象的数时间变化的函示跳水运动中高度随它表如图例21021056943112tttthttth0l1l2lthO0t1t2t311.图.,的变化情况刻画曲线在动点附近利用曲线在动点的切线.,,,变化情况在上述三个时刻附近的线刻画曲处的切线在我们用曲线解thtttxh210.,,.,几乎没有升降较平坦附近曲线比在所以轴平行于处的切线在曲线时当00001ttxltthtt.,,.`,附近单调递减在即函数降附近曲线下在所以的斜率处的切线在曲线时当11111102ttthttthltthtt.,,.`,单调递减附近也在即函数附近曲线下降在所以的斜率处的切线在曲线时当12222203ttthttthltthtt.,,.附近下降得缓慢附近比在在这说明曲线程度的倾斜的倾斜程度小于直线直线可见从图2121311ttthll0l1l2lthO0t1t2t311.图80.80.50.0010.20.30.40.60.70.90.01.11.10.20.30.40.50.60.70.90.01.11.mlmgc/mint411.图..,min...,.,.,.min:)/:(,.10806040204113精确到率物浓度的瞬时变化血管中药时估计根据图象函数图象变化的单位随时间位单物浓度表示人体血管中药它如图例ttmlmgtfc它表示从图象上看在此时刻的导数药物浓度就是度的瞬时变化率血管中某一时刻药物浓解,.,tf.在此点处的切线的斜率曲线tf.,,,.时变化率的近似值瞬可以得到此刻药物浓度估计这条切线的斜率利用网格线画出曲线上某点处的切如图411...,.,.'41804180ft所以它的斜率约为处的切线作.,,这些值是否正确一下验证时变化率的估计值下表给出了药物浓度瞬417004080604020.......'tft药物浓度的瞬时变化率.lim,).()(,,,.,,0''''0'00xxfxxfyxfyxfyfunctionderivativexfxxfxxfxxxxxfx即的导函数有时也记作简称的们称它为我的一个函数便是变化时当样这是一个确定的数时当看到处导数的过程可以在从求函数导函数导数