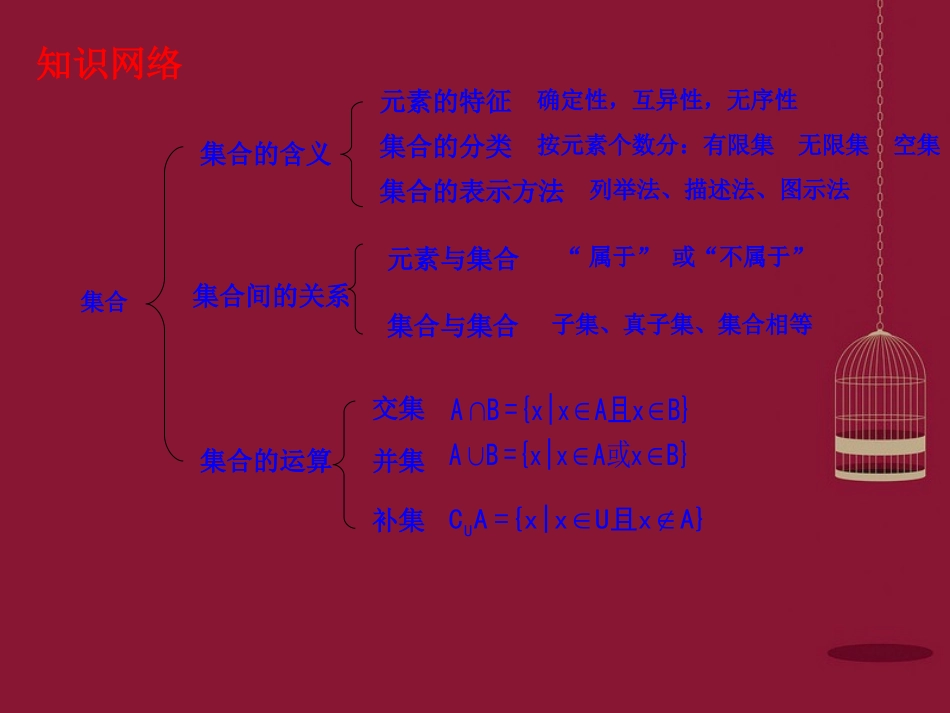
知识网络集合集合的含义元素的特征集合的分类集合的表示方法集合间的关系元素与集合集合与集合集合的运算交集并集补集确定性,互异性,无序性AB={x|xA且xB}或AB={x|xAxB}UCA={x|xU且xA}列举法、描述法、图示法“属于”或“不属于”子集、真子集、集合相等按元素个数分:有限集无限集空集特别提示:解答集合问题,必须准确理解集合的有关概念,对于用描述法给出的集合,要紧紧抓住分隔符前面的代表元素x以及CCCCCCI它所满足的条件P,例如:命题角度1:集合概念的理解及元素的特性1{(,)|0,,},{|1,,},MxyxyxRyRNxxyxRyRMN例、集合则集合中元素的个数()A.0B.1C.2D.3{(,)|0,,},{)|1,,},MxyxyxRyRNxyxyxRyRMN变式:集合(,则集合中元素的个数()A.0B.1C.2D.3AB|2,|2|0xxAxyRByyyy而|xxP1:PQP+Q=abapbQ,P=025Q=126P+QA.8B.9C.7D.6Ex设,为两个非空实数集合,定义集合+|,若,,,,,则中元素的个数是()A22.2,25,123Aa=ExAaaa已知集合且-,则2-3-3=2253a.Aaaa分析由得或,求出后再进行验证关键:验证求出的a值是否满足集合中元素的“互异性”3-2命题角度1:集合概念的理解及元素的特性命题角度2:子集与真子集的概念1(2007)P=12QPQ例:年,中山模拟已知集合,,那么满足的集合的个数()A.4B.3C.2D.1AP变式:满足Q的集合Q的个数是()B,____Pn引申:若有限集中有个元素P的子集个数为2n____P的真子集个数为21n特别提示:(1)空集是任何集合的子集;是任何非空集合的真子集(2)任何集合都是它本身的子集_________的非空真子集个数P22n实数2例2:集合A={x|x-3x+2=0},B={x|ax-2=0}若A∪B=A,求a.处类问题两处对为进讨论思路分析:理此有值得注意:2(1)A∪B=ABA;(2)B={x|ax-2=0}≠{x|x=}a要注意a是否0行。当时时当时为2解:A=x|x-3x+2=0={1,2},A∪B=ABAa=0,B=,此A,符合要求2a≠0,B={x|ax-2=0}={x|x=}a22∵BA∴=1或=2aa解得a=2或a=1所以a的值0,1或2。化归思想分类讨论思想命题角度2:子集与真子集的概念命题角度3集合的运算1:(20065602...ExxBCD2年)已知集合A=x|x,集合B=x|x<-1或x,则集合AB=()A.x|2x3x|2x<3x|2