高中数学(数列)复习课件新人教A版必修5 课件VIP免费

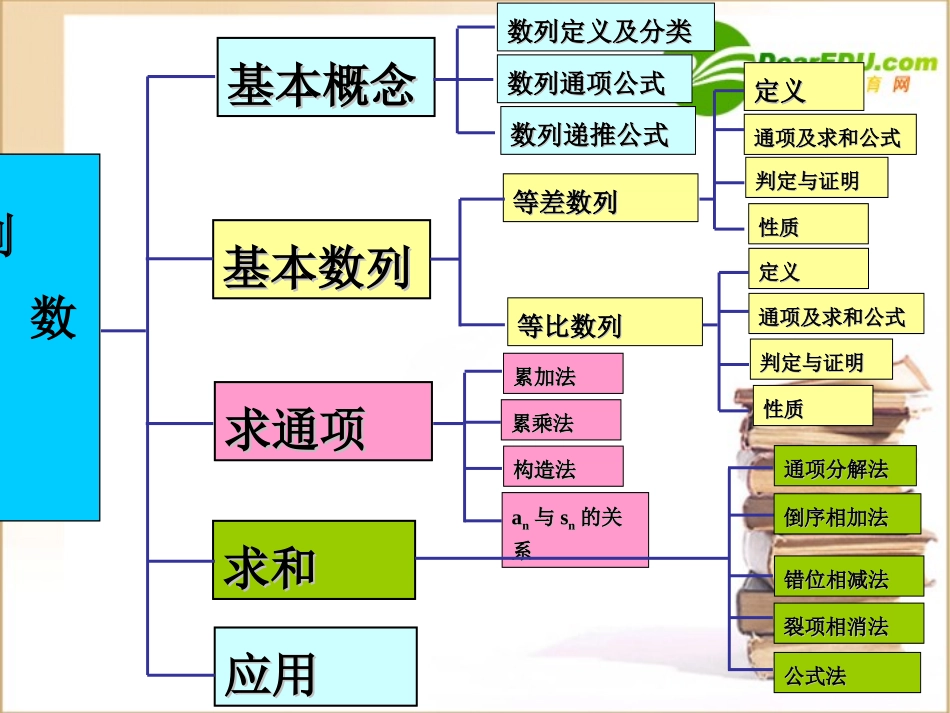
数列复习数列复习数列基本概念基本概念基本数列基本数列求通项求通项求和求和应用应用数列定义及分类数列定义及分类数列通项公式数列通项公式数列递推公式数列递推公式等差数列等差数列等比数列等比数列定义定义通项及求和公式通项及求和公式判定与证明判定与证明性质性质累加法累加法累乘法累乘法构造法构造法aann与与ssnn的关的关系系定义定义通项及求和公式通项及求和公式判定与证明判定与证明性质性质通项分解法通项分解法错位相减法错位相减法裂项相消法裂项相消法公式法公式法倒序相加法倒序相加法大于小于大于小于1nna1,1,1,1,111,）练习：写出下面数列的一个通项公式，使它的前几项分别是下列各数：51019nna5,55,555,55565,）2)512nna2,3,2,3,2,3,3）23nnan为正奇数为正偶数,,,,,,,ababab1122nnababa知识点：知识点：1、定义：2、通项公式：为等差数列}{nana推广：nanSn:.3项和公式前nnnnSaaa为等差数列为等差数列）（重要结论：}){2(}{1.4dna)1(1二、等差数列二、等差数列dmnam)(bknBnAn2常数nnaa12)(1naandnnna2)1(15.等差数列性质：（1）nmaanmd（2）若mnpq则mnpqaaaanmaadnmdkd2（3）若数列是等差数列，则也是等差数列}{na,,,,34232kkkkkkkSSSSSSS（4）等差数列{an}的任意等距离的项构成的数列仍为等差数列•等差数列判定方法：（1）定义法：（2）等差中项法：（3）看通项法：（4）看前n项和法：1nnaa常数,naknbkb（其中为常数）112nnnaaa2()nSAnBnAB、为常数15151284122saaaaa求,.na为等差数列1.1379511374sdaaaaa,,,,,求921003aas则,.5.在等差数列{an}中，S10=100，S100=10，求S110.,.421147anama，求练习：2nm00=-30=-30=-110=-110-3-3；；22；；-5/2-5/2；；22667.已知是两个等差数列，前项和,nnab88.ab分别是和且nAn,nB72,3nnAnBn求181073152157151588BAba1212nnnnBAba12121211212121nnnnnaaABnbb212212nnnnnaanbb是等比数列若重要结论：项和公式前推广：通项公式：为等比数列、定义：}{.4:.3________________.2________}{1nnnnnaSnaaa11nnaaq)1()1(1)1(11qnaqqqan三、等比数列三、等比数列常数nnaa1mnmqannkqa5.等比数列的性质（2）,qpnm若qpnmaaaa则（1）mnmnqaamnmnaaqq求（3）若数列是等比数列，则也是等比数列}{na,,,,34232kkkkkkkSSSSSSSkqq（4）等比数列{an}的任意等距离的项构成的数列仍为等比数列•等比数列判定方法：（1）定义法：（2）递推公式法：（3）看通项法：（4）看前n项和法：常数nnaa1211nnnaaannkqannSkkq1、在等比数列中，na（1）若则485,6,aa210aa（2）若则5102,10,aa15a（4）若则1234324,36,aaaa56aa6a（3）已知求3458,aaa23456.aaaaa=305032430练习：*1221,0)1(,0,11Nnaanaanaannnnn)2(33,3111naaaannn)(1nfaann)(1nfaannbkaann1五、已知数列递推公式求通项公式：五、已知数列递推公式求通项公式：111nnbkbakakk取倒数：如累加法累加法累乘法累乘法构造法构造法分解因式：分解因式：如如an与sn的关系)1(22,1)3(11nnaaaannn)2(3,1)2(211naaann练习：求数列通项公式na（分解因式）（分解因式）（取倒数、累加）（取倒数、累加）1111,1()22.nnnaaanNa1.已知求（构造新数列）（构造新数列）(1)设数列前项的和nan2231,nSnn求的通项公式.na设数列的前项和，nannS即1112nnnSnaSSn123nnSaaaa则知和求项:2,141,6nnnan数列中，，前n项的和求设正项数列满足，（n≥2）.的通项公...