高中数学 抛物线的简单几何性质课件 新人教A版选修1 课件VIP免费

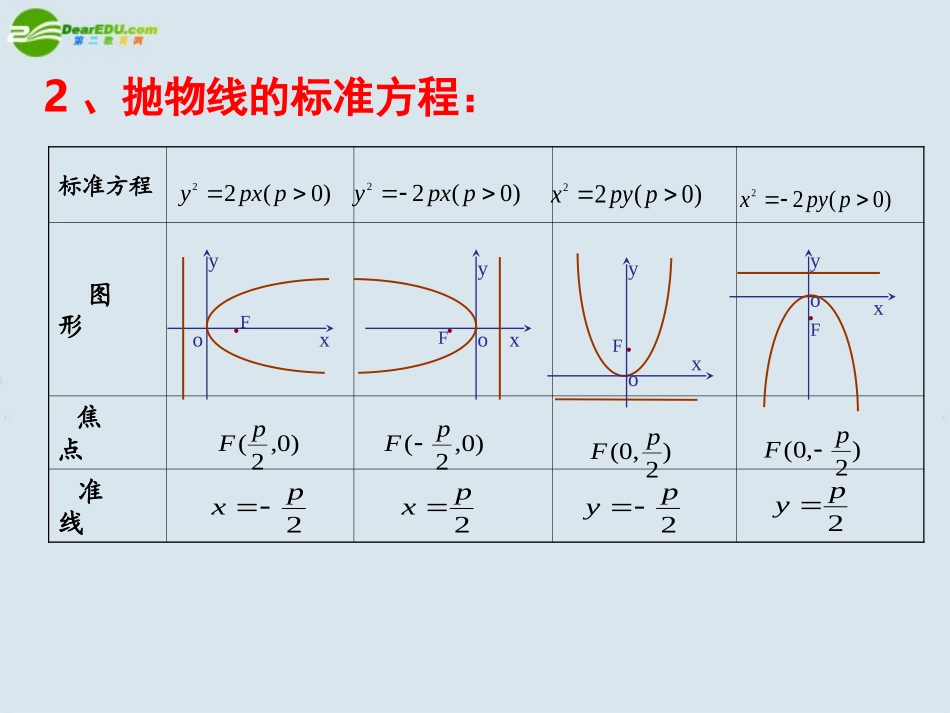
一、复习回顾：l.FMd.xOyK－－抛物线标准方程0p是焦准距22ypx1、抛物线的定义：平面内与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫做抛物抛物线线。定点F叫做抛物线的焦点焦点。定直线l叫做抛物线的准准线线。标准方程图形焦点准线)0(22ppxy)0(22ppyxxyoF..xyFo)0,2(pF.yxoF2px)2,0(pF.xoyF2py)0(22ppxy)0,2(pF2px)0(22ppyx)2,0(pF2py2、抛物线的标准方程：例例11求下列抛物线的焦点坐标和准线方程求下列抛物线的焦点坐标和准线方程(1)y(1)y22=6x=6x（（22））（（33））2x2x22+5y=0+5y=0（3）抛物线方程是2x2+5y=0,即x2=-y,2p=2525则焦点坐标是F（0，-）,准线方程是y=858533:(,0),22x解(1)焦点坐标准线方程yx21218y(2)焦点坐标是准线方程是81,0练习：1、根据下列条件，写出抛物线的标准方程：（1）焦点是F（3，0）；（2）准线方程是x=；41（3）焦点到准线的距离是2。y2=12xy2=xy2=4x、y2=-4x、x2=4y或x2=-4y2、求下列抛物线的焦点坐标和准线方程：（1）y2=20x（2）x2=y（3）2y2+5x=0（4）x2+8y=0焦点坐标准线方程（1）（2）（3）（4）（5，0）x=-5（0，—）116y=-—1168x=—5（-—，0）58（0，-2）y=241例例22根据下列条件写出抛物线的标准方程：根据下列条件写出抛物线的标准方程：(1)(1)焦点坐标是焦点坐标是FF（（00，，-2-2））(2)(2)焦点在直线焦点在直线3x-4y-12=03x-4y-12=0上上(3)(3)抛物线过点抛物线过点AA（（-3-3，，22））解：解：(1)(1)抛物线的方程是抛物线的方程是xx22=-8y=-8y(2)(2)抛物线的方程是抛物线的方程是yy22=16x=16x或或xx22=-12y=-12y(3)(3)当抛物线的焦点在当抛物线的焦点在yy轴的正半轴上时，轴的正半轴上时，把把AA（（-3-3，，22）代入）代入xx22=2py=2py，，当焦点在当焦点在xx轴的负半轴上时，轴的负半轴上时，把把AA（（-3-3，，22）代入）代入yy22=-2px=-2px，，得得p=p=9494∴∴抛物线的标准方程为抛物线的标准方程为xx22=y=y或或yy22=-x=-x92924343oxyA2323得得p=p=思考题：抛物线的方程为x=ay2（a≠0)求它的焦点坐标和准线方程？抛物线的方程为x=ay2（a≠0)求它的焦点坐标和准线方程？解：抛物线标准方程为：y2=x1a∴2p=1a4a1∴焦点坐标是（，0），准线方程是：x=4a1②当a<0时,,抛物线的开口向左p2=14a∴焦点坐标是（，0），准线方程是：x=4a114a①当a>0时,,抛物线的开口向右p2=14a例5点M到点F(4，0)的距离比它到直线l:x+5=0的距离小1，求点M的轨迹方程。|MF|+1=|x+5|ly..oxMF解（直接法）：设M(x，y)，则由已知，得51)4(22xyx即化简得xy162.的轨迹方程即为点M另解(定义法)：由已知，得点M到点F(4，0)的距离等于它到直线l:x+4=0的距离.由抛物线定义知：点M的轨迹是以F(4，0)为焦点的抛物线.，42p.8p.162xyM的轨迹方程为故点【讲授新课】【讲授新课】结合抛物线y2=2px(p>0)的标准方程和图形,探索其的几何性质:(1)范围(2)对称性(3)顶点类比探索x≥0,yR∈关于x轴对称,对称轴又叫抛物线的轴抛物线和它的轴的交点.二、讲授新课：.yxoF(4)离心率抛物线上的点与焦点的距离和它到准线的距离的比，叫做抛物线的离心率，用e表示，由抛物线的定义可知，e=1只有一个顶点方程图形范围对称性顶点离心率y2=2px（p＞0）y2=-2px（p＞0）x2=2py（p＞0）x2=-2py（p＞0）lFyxOlFyxOlFyxOx≥0yR∈x≤0yR∈xR∈y≥0y≤0xR∈lFyxO关于x轴对称关于x轴对称关于y轴对称关于y轴对称（0,0）e=1补充（1）通径：通过焦点且垂直对称轴的直线，与抛物线相交于两点，连接这两点的线段叫做抛物线的通径。|PF|=x0+p/2xOyFP通径的长度：2PP越大,开口越开阔图.gsp（2）焦半径：连接抛物线任意一点与焦点的线段叫做抛物线的焦半径。焦半径公式：),(00yx（标准方程中2p的几何意义）利用抛物线的顶点、通径的两个端点可较准确画出反映抛物线基本特征的草图。基本点：顶点，焦点基本点：顶点，焦点基本线：准线，对称轴基本线：准线，对称轴基本量：基本量：PP（决定（决定抛物线开口大小）抛物线开口大小）XY抛物线的基本元素y2=2px填空练习：与椭圆、双曲线的几何性质比较...