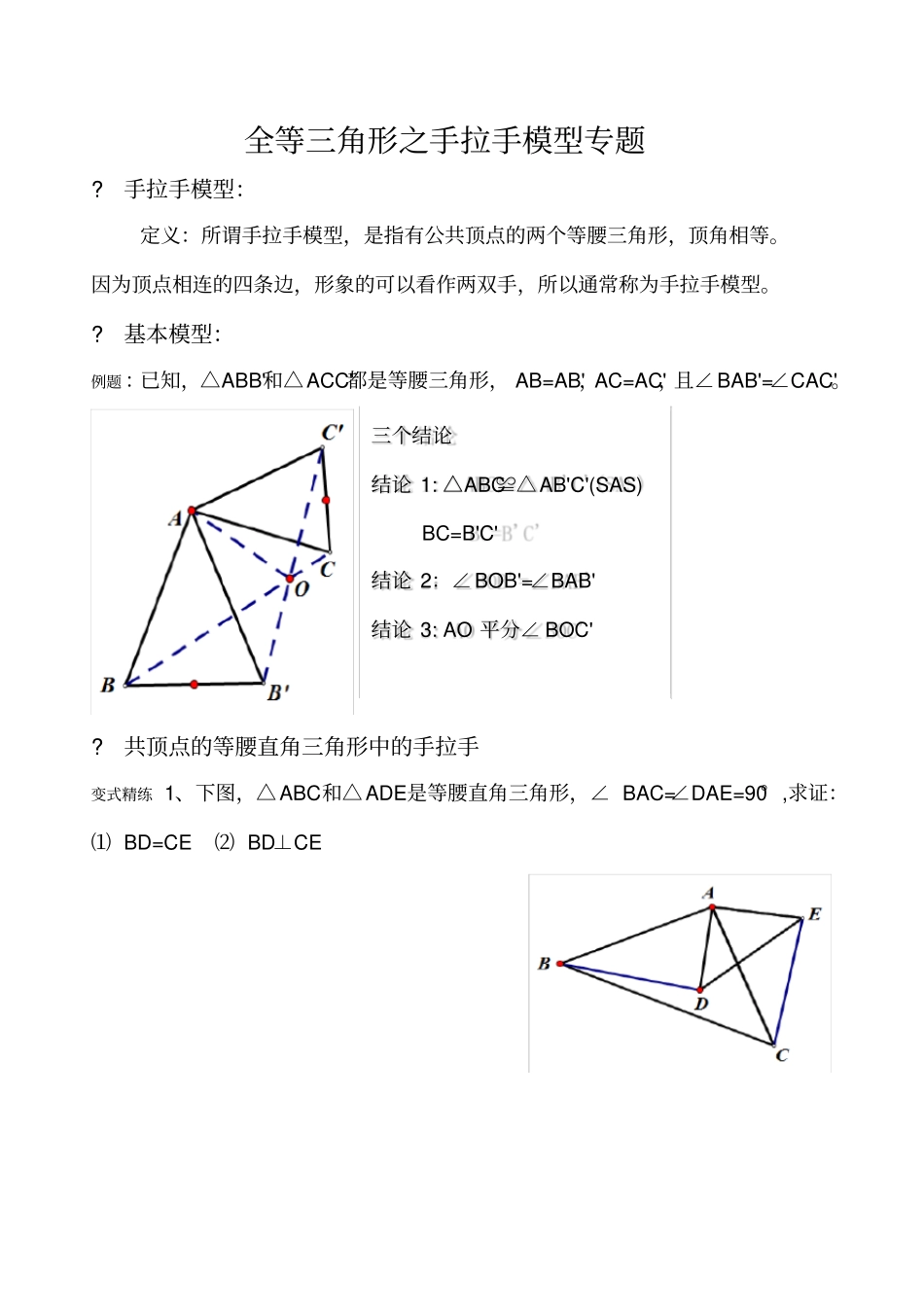
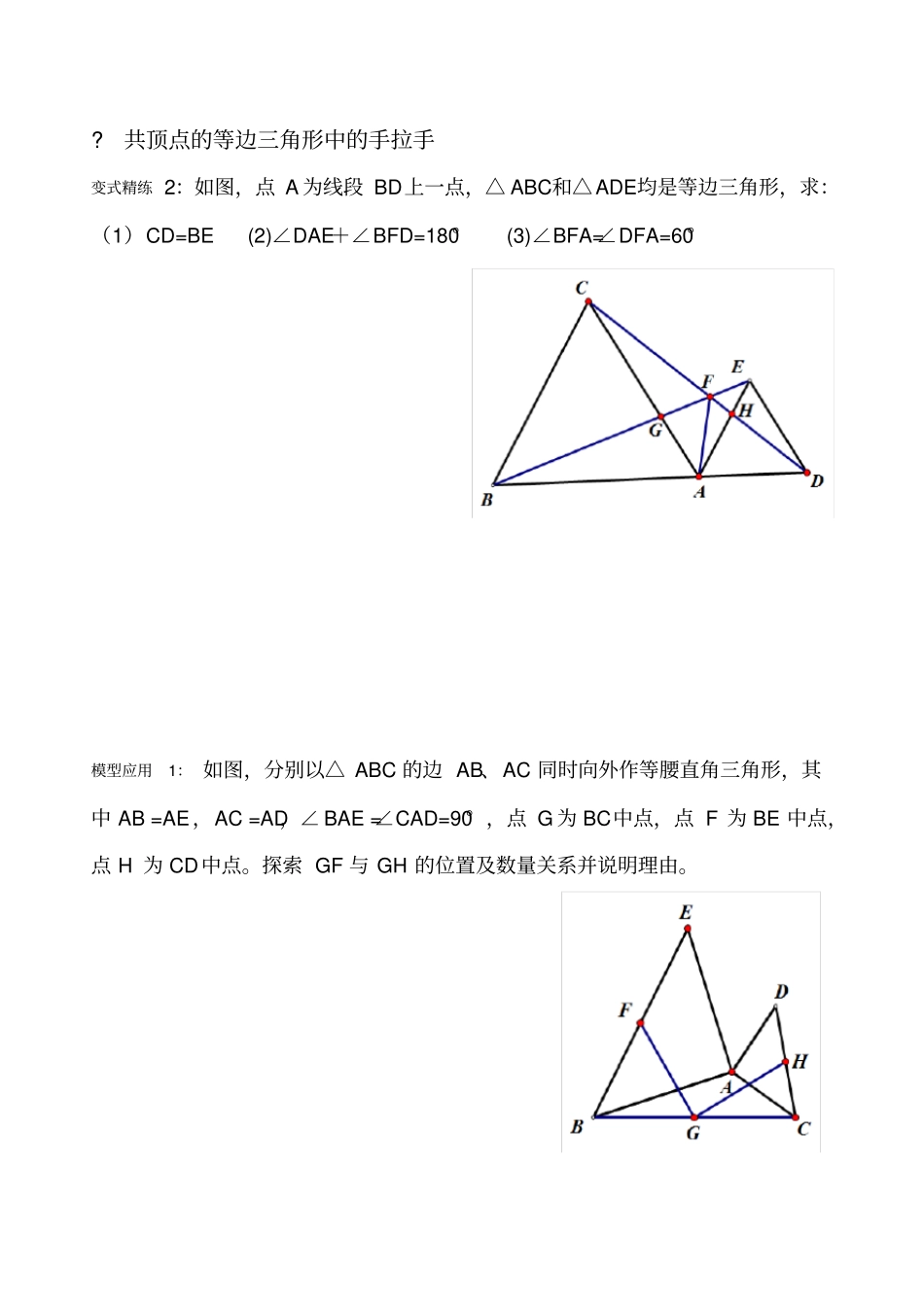
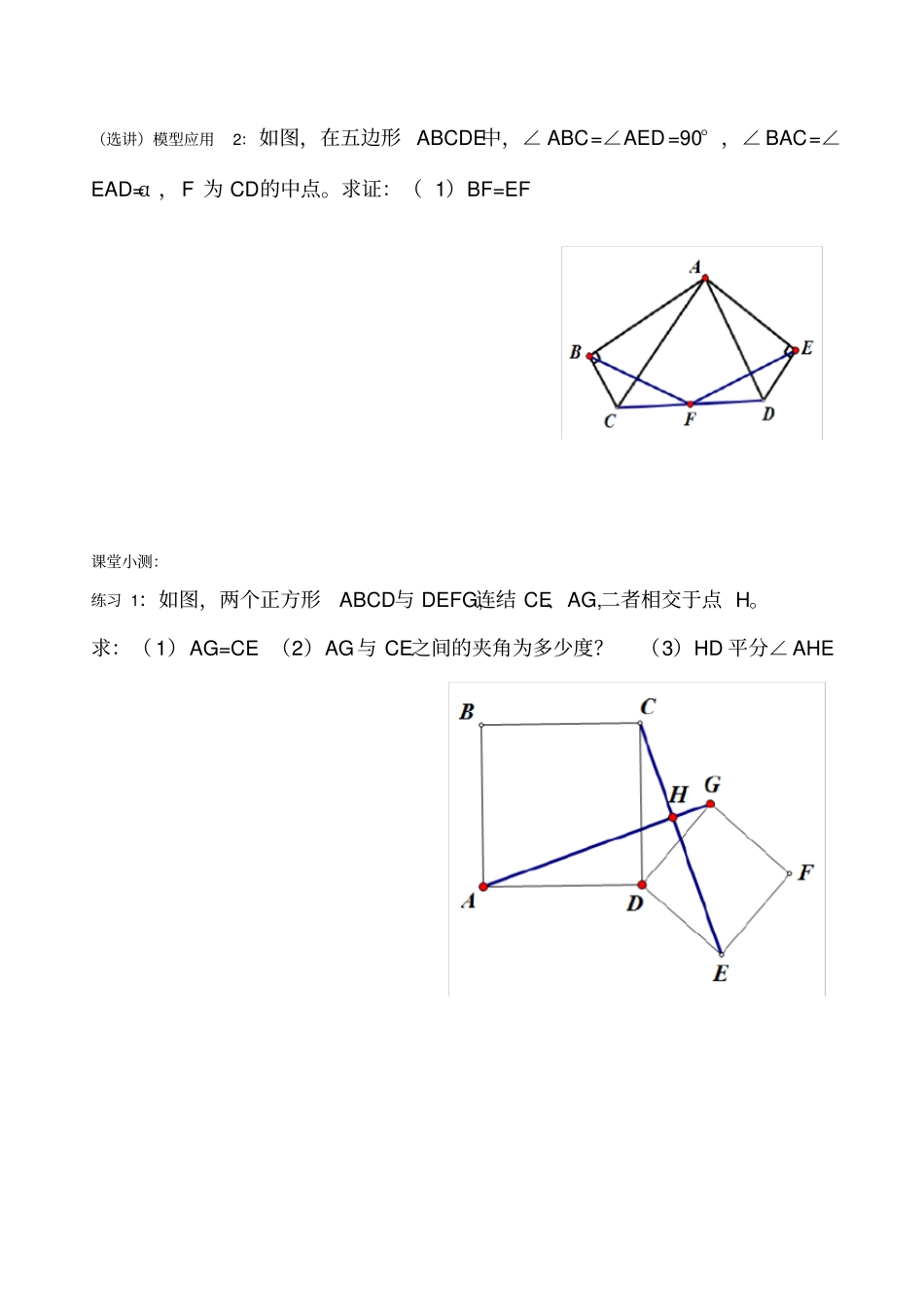
全等三角形之手拉手模型专题?手拉手模型:定义:所谓手拉手模型,是指有公共顶点的两个等腰三角形,顶角相等。因为顶点相连的四条边,形象的可以看作两双手,所以通常称为手拉手模型。?基本模型:例题:已知,△ABB'和△ACC'都是等腰三角形,AB=AB',AC=AC',且∠BAB'=∠CAC'。?共顶点的等腰直角三角形中的手拉手变式精练1、下图,△ABC和△ADE是等腰直角三角形,∠BAC=∠DAE=90°,求证:⑴BD=CE⑵BD⊥CE三个结论结论1:△ABC≌△AB'C'(SAS)BC=B'C'结论2:∠BOB'=∠BAB'结论3:AO平分∠BOC'?共顶点的等边三角形中的手拉手变式精练2:如图,点A为线段BD上一点,△ABC和△ADE均是等边三角形,求:(1)CD=BE(2)∠DAE+∠BFD=180°(3)∠BFA=∠DFA=60°模型应用1:如图,分别以△ABC的边AB、AC同时向外作等腰直角三角形,其中AB=AE,AC=AD,∠BAE=∠CAD=90°,点G为BC中点,点F为BE中点,点H为CD中点。探索GF与GH的位置及数量关系并说明理由。(选讲)模型应用2:如图,在五边形ABCDE中,∠ABC=∠AED=90°,∠BAC=∠EAD=α,F为CD的中点。求证:(1)BF=EF课堂小测:练习1:如图,两个正方形ABCD与DEFG,连结CE、AG,二者相交于点H。求:(1)AG=CE(2)AG与CE之间的夹角为多少度?(3)HD平分∠AHE