高中数学 抛物线几何性质2课件 新人教版选修2-1 课件VIP免费

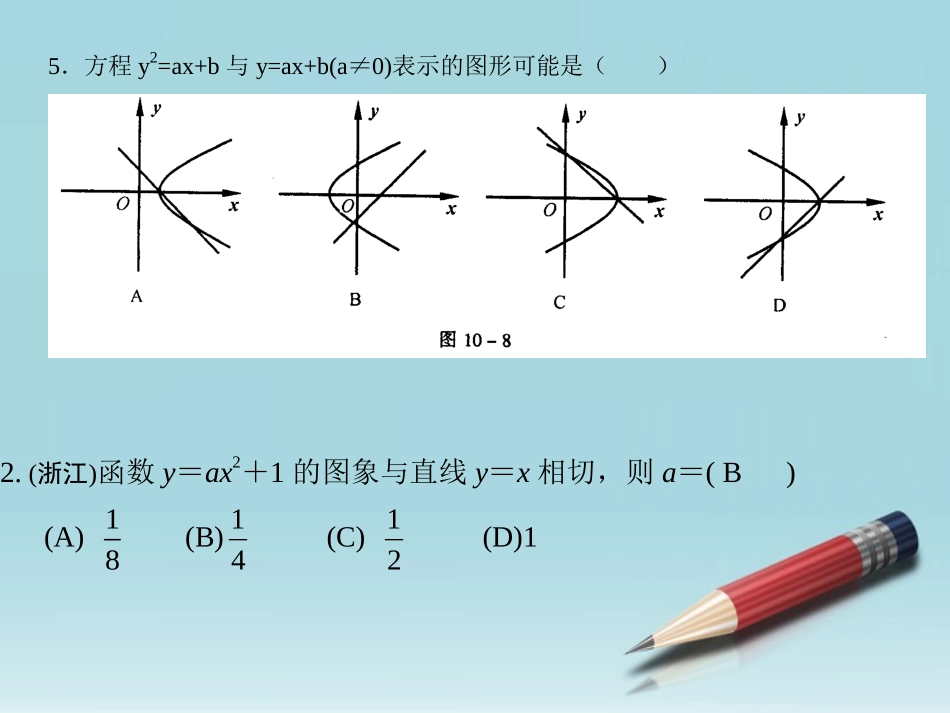
例5过抛物线焦点F的直线交抛物线于A,B两点，通过点A和抛物线顶点的直线交抛物线的准线于点D，求证：直线DB平行于抛物线的对称轴。,22pxyx物线的方程为建立直角坐标系。设抛轴，它的顶点为原点，轴为证明：以抛物线的对称,2),,2(0020xypyOAypyA的方程为则直线的坐标为点2px抛物线的准线是.02ypyD的纵坐标为联立可得点.222),0,2(200ppypxyyAFpF方程为的所以直线的坐标是因为点.02ypyB的纵坐标为联立可得点轴。所以xDB//xyOFABD5.（上海）过抛物线xy42的焦点作一条直线与抛物线相交于A、B两点，它们的横坐标之和等于5，则这样的直线（B）A．有且仅有一条B．有且仅有两条C．有无穷多条D．不存在12．给出下列结论,其中正确的是（）A．渐近线方程为0,0baxaby的双曲线的标准方程一定是12222byaxB．抛物线221xy的准线方程是21xC．等轴双曲线的离心率是2D．椭圆0,012222nmnymx的焦点坐标是0,,0,222221nmFnmF5．方程y2=ax+b与y=ax+b(a≠0)表示的图形可能是（）2.(浙江)函数y＝ax2＋1的图象与直线y＝x相切，则a＝(B)(A)18(B)41(C)21(D)16．抛物线)0(22ppxy上有),,(),,(2211yxByxA),(33yxC三点，F是它的焦点，若CFBFAF,,成等差数列，则()A．321,,xxx成等差数列B．231,,xxx成等差数列C．321,,yyy成等差数列D．231,,yyy成等差数列9.AB是抛物线x=y2的一条焦点弦，且｜AB｜=4，则AB的中点到直线x+1=0的距离为()A.25B.2C.3D.411例1已知抛物线的方程为y²=4x,直线l过定点P(-2,1)，斜率为k,k为何值时，直线l与抛物线y²=4x:只有一个公共点；有两个公共点；没有公共点？).2(1xkyl的方程为解：由题意，设直线xyxky4)2(12由方程组0)12(442kyky可得.10)1(yk时，由方程得当.41,412xxyy得代入把)1,41(点与抛物线只有一个公共这时，直线lXYO·P例1已知抛物线的方程为y²=4x,直线l过定点P(-2,1)，斜率为k,k为何值时，直线l与抛物线y²=4x:只有一个公共点；有两个公共点；没有公共点？).2(1xkyl的方程为解：由题意，设直线xyxky4)2(12由方程组0)12(442kyky可得).12(160)2(2kkk＝时，方程的判别式为当0120120kk，即＝由.21,1kk或解得个公共点。即直线与抛物线只有一，时，方程组只有一个解，或即当211kk0120220kk，即由.211k解得公共点。即直线与抛物线有两个时，方程组有两个解，且即当0,211kk0120320kk，即由.211kk，或解得共点。即直线与抛物线没有公，时，方程组没有实数解或即当211kk个公共点。即直线与抛物线只有一时，，或，或综上所述，当0211kkk公共点。即直线与抛物线有两个时，且当0,211kk共点。即直线与抛物线没有公时，或当211kk直线与抛物线有一个公共点的情况有两种情形：一种是直线平行于抛物线的对称轴；另一种是直线与抛物线相切．l1l2例题1.如图所示，直线与相交于M点，以A,B为端点的曲线段C上的任一点到的距离与到点N的距离相等，为锐角三角形，建立适当坐标系,求曲线C的方程。1l2l21ll2lNAMN6,3,17BNANAM1lBAMN123分析：1.如何选择适当的坐标系。2.能否判断曲线段是何种类型曲线。3.如何用方程表示曲线的一部分。l1l2例题1.如图所示，直线与相交于M点，以A,B为端点的曲线段C上的任一点到的距离与到点N的距离相等，为锐角三角形，建立适当坐标系,求曲线C的方程。1l2l21ll2lNAMN6,3,17BNANAM1lyxD解法一：1NCACNRt中，)0,2(,4为则NMN8222pp得由图得，），为（221A），为（244BCBAMN曲线段C的方程为：)0,41(82yxxy即抛物线方程：xy823,ANADMCACMRt2217ACAM，则且l1l2例题1.如图所示，直线与相交于M点，以A,B为端点的曲线段C上的任一点到的距离与到点N的距离相等，为锐角三角形，建立适当坐标系,求曲线C的方程。1l2l21ll2lNAMN6,3,17BNANAM1lyxDCBAMN42,或得p解法二：)0(22ppxy设抛物线方程：)22,23(pA)23(28ppNAxxAMN为锐角三角形，43223...