高中数学 正余弦定理2教学课件 新人教A版必修5 课件VIP免费

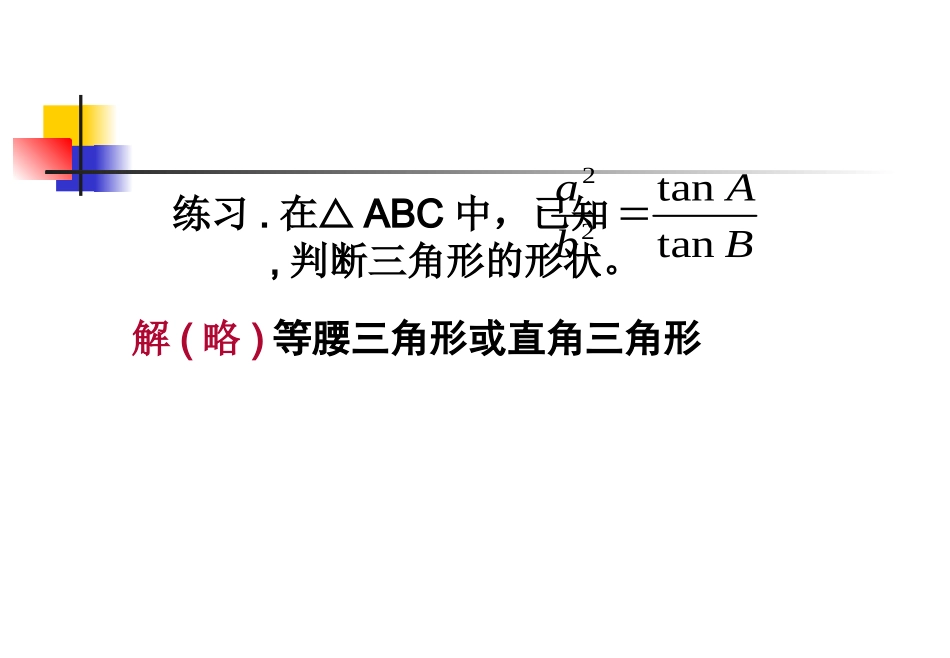
正弦定理及其变形RCcBbAa2sinsinsin边角分离ARasin2BRbsin2CRcsin2AbcBacCabSABCsin21sin21sin21BAbatantan22练习.在ABC中，已知,判断三角形的形状。解(略)等腰三角形或直角三角形练习2，在△ABC中，已知（a+b+c)(b+c-a)=3bc,且sin2A=sinBsinC,判断三角形的形状。一、要点复习：余弦定理CabbacBcaacbAbccbacos2cos2cos2222222222变形abcbaCcabacBbcacbA2cos2cos2cos222222222222bacRt中，在二、余弦定理应用（1）已知三边（2）已知两边和夹角CabbacBcaacbAbccbacos2cos2cos2222222222.,150,2,33.3;,21,29,20.2;,6038.1bBcaBcbaaAcbABC求已知求已知求，，已知中，在练习题答案:1.7;2.90°;3.7.在三角形中,已知(a+b)(a-b)=c(b+c),求角A.问题2：解：条件整理变形得CABacb212222bcacb即21cosAA=1200动手实践：在ABC中，已知accba2222,求角B.bcacb222变式3：在ABC中，已知）（ABACBsinsin2sinsinsin22求角C.开拓创新：1.在ABC中，证明:ACBCBAcossinsin2sinsinsin2222.求的值.10sin20sin310sin20sin22例4在△ABC中，a、b、c分别是A、B、C的对边，试证明：a=bcosC+ccosB证明：由余弦定理知：，abcbaC2cos222cabacB2cos222右边=cabaccabcbab22222222abacacba22222222aa222左边aABCDcba三，已知三角形形状，讨论边的取值范围。bacacbcbacbaABC,,,,1的三边为2当△ABC直角三角形时（c>a>b）222bac当△ABC为钝角三角形时（c>b>a）0222cba当△ABC为锐角三角形时（c>b>a）0222cba当△ABC为锐角三角形时000222222222bacacbcba例1，a,a+1,a+2构成钝角三角形，求a的取值范围。例2，锐角三角形的三边长为2,x,3，求x的取值范围。练习：三条线段长度为2,x,6(1)求构成直角三角形时，x的取值范围(2)求构成锐角三角形时，x的取值范围(3)求构成钝角三角形时，x的取值范围例题精选例3已知△ABC的三内角A、B、C成等差，而A、B、C三内角的对边a、b、c成等比.试证明：△ABC为正三角形.证明：∵a、b、c成等比，∴b2=ac∵A、B、C成等差，∴2B=A+C，又A+B+C=180o，∴B=60o，A+C=120o又由余弦定理得：accaaccaBaccab222222260cos2cos2∴accaac22，即0)(2ca，∴a=c又∵B=60o，∴△ABC是正三角形.例题精选例4在△ABC中，如果，并且B为锐角，试判断此三角形的形状特征。2lgsinlglglgBca解：由，2lgsinlglglgBca得：22sinBB=45o22ca22sinsinCA，将A=135o-C代入上式，得)135sin(2sin2CCCCCcossinsin∴C=90o，综上所述，△ABC是等腰直角三角形。例题精选例5在△ABC中，已知，且则∠B等于多少？,2,1BCAB3252BCAB答案：∠B=30o本课小测1、在△ABC中，一定成立的等式是（）（A）asinA=bsinA（B）asinB=bsinA（C）acosA=bcosB（D）acosB=bcosA2、在△ABC中，A>B是sinA>sinB的（）（A）充分不必要条件（B）必要不充分条件（C）充要条件（D）既不充分也不必要条件3、在△ABC中，若A：B：C=3：4：5，则a：b：c等于（）（A）（B）（C）（D）5:4:3)13(:6:22:3:1223:3:2本课小测4、在△ABC中，A=60o，b=1，S△ABC=？3CBAcbasinsinsin5、已知△ABC中，满足acosA=bcosB，试判断△ABC的形状。练习1在△ABC中，已知1）A=120o，B=30o，a=8，求c；2）a=14，b=7，B=，求A；3）b=，c=，A=120o，求a；4）a=2，b=3，c=，求C63357经验：根据已知条件适当选用正弦定理、余弦定理。