高中数学(两角和与差的正弦、余弦、正切)课件23 新人教A版必修4 课件VIP免费

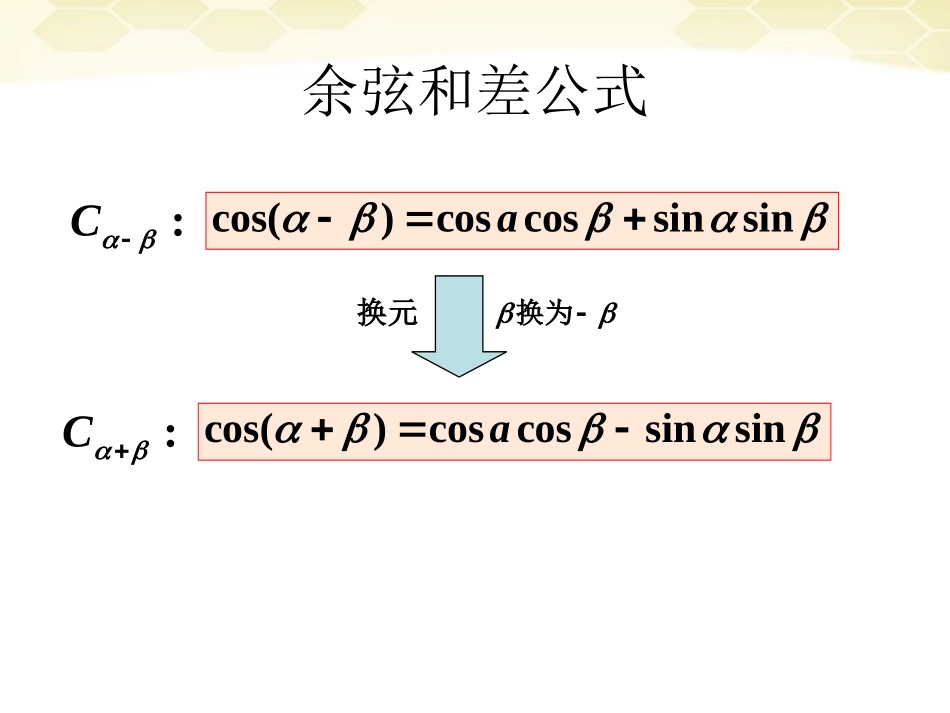
3.1.2两角和与差的正弦、余弦、正切公式第一课时2.||||ababab求证：(1证：)"明"ababab0abab||||abab22||||abab22()()abab222()2ababab22ab222()2ababab22ab||||abab2()""22||||abab222222abababab0abab矩形的对几何意义：角线相等余弦和差公式cos()coscossinsina:C换元换为cos()coscossinsina:C练习233sin,(,),cos,,cos()324IV已知：求23sin,(,)32解：5cos33cos,4IV7sin4cos()coscossinsin3527()()()4334273512探究：如何由余弦公式推出正弦公式cos()coscossinsin:C换元换为2sin():Scos()sin2sincoscossin探究：如何由余弦公式推出正弦公式cos()coscossinsin:C换元换为2sin():Scos()sin2sincoscossin你能想出其他方法吗？探究：如何由余弦公式推出正弦公式sin()sincoscossin:S换元换为sin():Ssincoscossin探究：正切和差公式sintancostantan:tan()1tantanTtantan:tan()1tantanT小结cos()coscossinsincos()coscossinsinsin()sincoscossintantan:tan()1tantanTtantan:tan()1tantanTsin()sincoscossin不需记忆，但要了解3.1.2两角和与差的正弦、余弦、正切公式第二课时学习目标：1、两角和、差正弦和正切公式的推导过程2、两角和、差正弦和正切公式的简单运用两角差的余弦公式cos（––）=coscos++sinsin在上式中，若将在上式中，若将ββ替换成替换成-β-β，则可得，则可得::cos（-（-）)=coscos（-）+sinsin（-）cos（+）=coscos–sinsin即：两角和的余弦公式Cα+βCα-βsin2cossin2cos2cossin2sincos2cossincoscossinsin:Ssincoscossin两角和的正弦公式sin:Ssincoscossin得到代替用)sin(cos)cos(sinsinsincoscossinsin:S两角差的正弦公式两角和的正切公式sincoscossincoscossinsinαβαβαβαβsin()tan()cos()(αβαβαβ这里有什么要求？）提问：能否化简？sincoscossincoscoscoscos(coscossinsincoscoscoscosαβαβαβαβαβαβαβαβ又有什么要求？）tantan1tantan...