河北省定州地区高二数学独立重复试验的概率课件 人教版 课件VIP免费

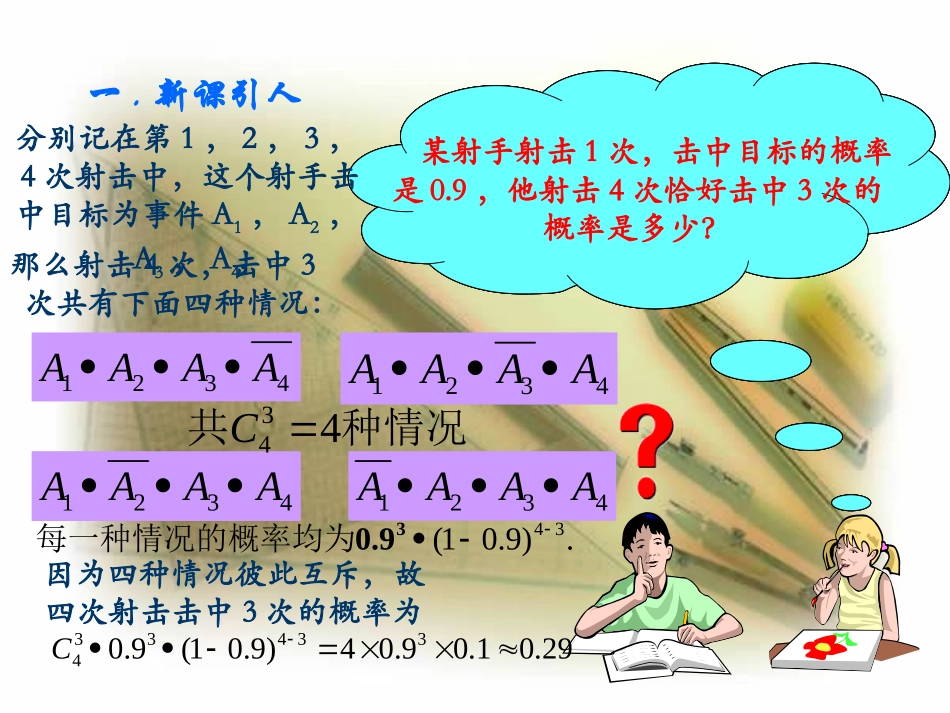
11.3.2独立重复试验的概率相互独立事件同时发生的概率XIANGHUDULISHIJIANTONGSHIFASHENGDEGAILV相互独立事件A、B同时发生的概率：P（A·B）=P（A）P（B）:复习某射手射击1次，击中目标的概率是0.9，他射击4次恰好击中3次的概率是多少？一.新课引人某射手射击1次，击中目标的概率是0.9，他射击4次恰好击中3次的概率是多少？某射手射击1次，击中目标的概率是0.9，他射击4次恰好击中3次的概率是多少？某射手射击1次，击中目标的概率是0.9，他射击4次恰好击中3次的概率是多少？某射手射击1次，击中目标的概率是0.9，他射击4次恰好击中3次的概率是多少？分别记在第1，2，3，4次射击中，这个射手击中目标为事件A1，A2，A3，A4,那么射击4次，击中3次共有下面四种情况：4321AAAA4321AAAA4321AAAA4321AAAA种情况共434C.)9.01(3430.9每一种情况的概率均为因为四种情况彼此互斥，故四次射击击中3次的概率为29.01.09.04)9.01(9.0334334C相互独立事件同时发生的概率XIANGHUDULISHIJIANTONGSHIFASHENGDEGAILV独立重复实验的定义：在同等条件下独立进行的重复实验一般地，如果在1次试验中某事件发生的概率是P，那么在n次独立重复试验中这个事件恰好发生k次的概率knkknnPPCkP)1()(项展开式中的第）（是1knPP1二项分布公式AAk＝0,1,2,…，n相互独立事件同时发生的概率XIANGHUDULISHIJIANTONGSHIFASHENGDEGAILV说明：⑴独立重复试验，是在同样的条件下重复地、各次之间相互独立地进行的一种试验；⑵每一次独立重复试验只有两种结果，即某事件要么发生，要么不发生，并且任何一次试验中发生的概率都是一样的；⑶n次独立重复试验中某事件恰好发生k次的概率公式就是二项式展开式的第k＋1项；nP]P)[(1⑷此公式仅用于独立重复试验．例1设一射手平均每射击10次中靶4次，求在五次射击中①击中一次，②第二次击中，③击中两次，④第二、三两次击中，⑤至少击中一次的概率．解、由题设，此射手射击1次，中靶的概率为0.4．①n＝5，k＝1，应用公式得②事件“第二次击中”表示第一、三、四、五次击中或击不中都可，它不同于“击中一次”，也不同于“第二次击中，其他各次都不中”，不能用公式．它的概率就是0.4．③n＝5，k＝2，④“第二、三两次击中”表示第一次、第四次及第五次可中可不中，所以概率为0.4×0.4＝0.16．⑤设“至少击中一次”为事件B，则B包括“击中一次”，“击中两次”，“击中三次”，“击中四次”，“击中五次”，所以概率为P(B)＝P5(1)＋P5(2)＋P5(3)＋P5(4)＋P5(5)＝0.2592＋0.3456＋0.2304＋0.0768＋0.01024＝0.92224．1－P5(0)相互独立事件同时发生的概率XIANGHUDULISHIJIANTONGSHIFASHENGDEGAILVP137例3相互独立事件同时发生的概率XIANGHUDULISHIJIANTONGSHIFASHENGDEGAILV1.有10门炮同时各向目标各发一枚炮弹,如果每门炮的命中率都是0.1,则目标被击中的概率约是()A0.55B0.45C0.75D0.65D109.01练习相互独立事件同时发生的概率XIANGHUDULISHIJIANTONGSHIFASHENGDEGAILV2.一射手对同一目标独立地进行4次射击,已知至少命中一次的概率为,则此射手射击一次的命中率是()ABCD8180313241528180)p1(14BE-mail:xulong110@s126.comQQE-mail:xulong110@s126.comQQ：：3888559938885599请多提宝贵意见！再见！