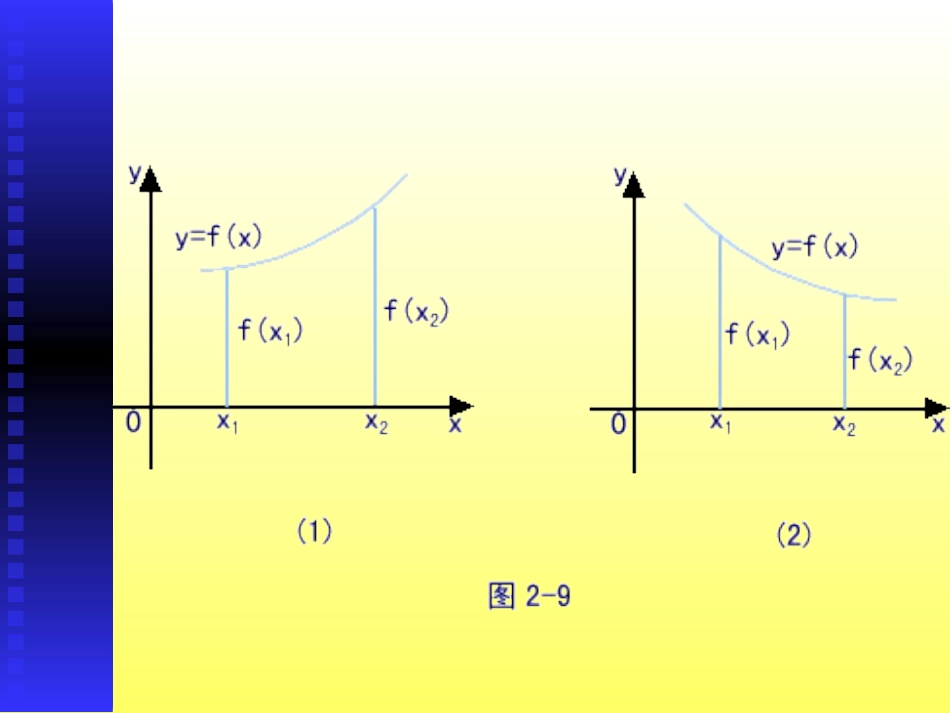
观察演示并思考问题:想看看函数的图象吗?函数的单调性.gsp函数单调性的概念:1.如果对于属于定义域I内某个区间的任意任意两个自变量),f(x)都有f(x时x当xx值x212121,,,称函数f(x)在这个区间上是增函数。2.如果对于属于定义域I内某个区间的任意自变量),f(x)都有f(x时,x当x,x,两个值x212121称函数f(x)在这个区间上是减函数。一般地,设函数f(x)定义域为I:观察函数的单调区间在X(0∈,+∞)为增函数在X(-∞∈,0)为减函数f(x)的单调区间有[-2,-1][-1,0][0,1][1,2]f(x)在区间[-2,-1][0,1]上是减函数f(x)在区间[-1,0][1,2]上是增函数求差可以判断两数大小关系,还有其他的方法吗?若f(1x)>0时,可用求商)2()1(xfxf的办法来比较,若)()(21xfxf大于1;则)(1xf>)(2xf若)2()1(xfxf小于1则)(1xf<)(2xf,从而判断商)2()1(xfxf与1的大小关系来判定函数单调性)(1xf)(1xf)(1xf证明函数f(x)=3x+2在R上是增函数证明:设1x,2x是R上任意两个实数,且1x<2x则)(1xf-)(2xf=(31x+2)-(32x+2)=31x+2-32x-2=3(1x-2x)∵1x<2x∴1x-2x<0∴)(1xf-)(2xf=3(1x-2x)<0∴函数f(x)=3x+2在R上是增函数例题一一..用定义证明函数单调性的用定义证明函数单调性的步骤:步骤:1.1.取值取值2.2.作差变形作差变形3.3.定号定号4.4.判断判断2121,xxxx且两个数在指定的区间上任意取)()(21xfxf函数的单调性练习.gsp4。小结(1)函数的单调性的概念理解①单调性相对特定的区间而言②定义中X1,X2有以下的特点⑴X1、X2有区间上⑵X1、X2任意性⑶X1