高一数学 241平面向量的数量积及运算律课件VIP免费

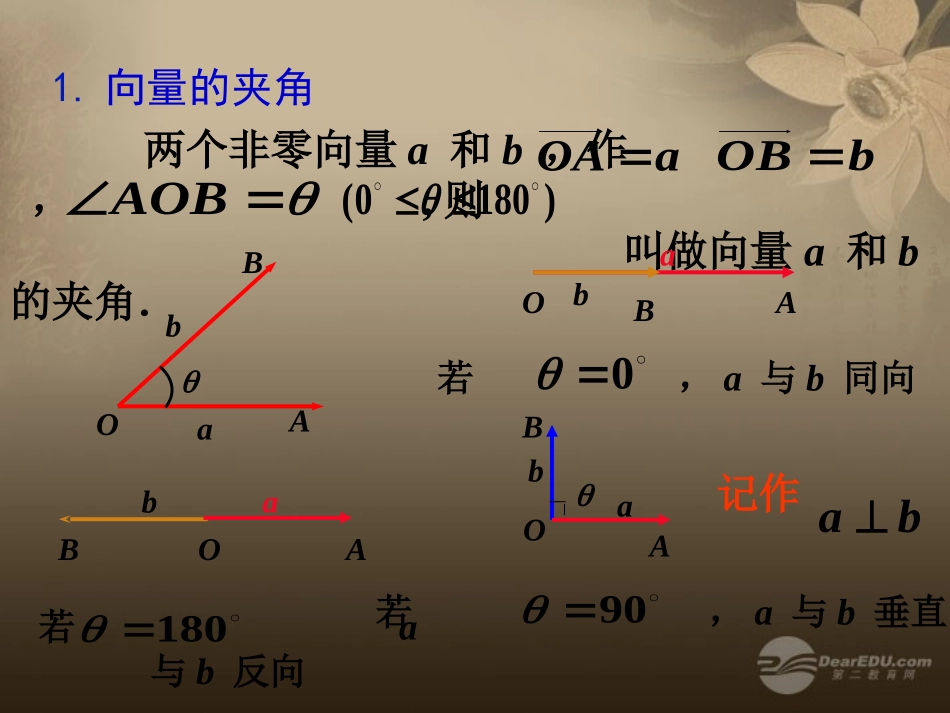
平面向量的数量积引入:我们学过功的概念，即一个物体在力F的作用下产生位移s（如图）θFS力F所做的功W可用下式计算W=|F||S|cosθ其中θ是F与S的夹角从力所做的功出发，我们引入向量数量积的概念。两个非零向量a和b，作，,则叫做向量a和b的夹角．aOAbOBAOB)1800(OABabOABba若，a与b同向0OABba若a与b反向180OABab若，a与b垂直，90ba记作1.向量的夹角练习1、如图，等边三角形中，求（1）AB与AC的夹角；（2）AB与BC的夹角。ABC通过平移变成共起点！12060'C2.平面向量的数量积的定义cos||||baba规定：零向量与任意向量的数量积为0，即0．0acos||||ba已知两个非零向量a和b，它们的夹角为，我们把数量叫做a与b的数量积（或内积），记作a·b，即注意：(1)两向量的数量积是一个数量，而不是向量，符号由夹角决定(2)a·b不能写成a×b(3)向量的数量积与实数积的区别:2）对于实数a、b、c（b≠0），若a·b=b·c，则a=c,对于向量a，b，c,此式是否仍成立呢？1)对实数a≠0,若a·b=0，则b=0，但对向量a≠0时，若a·b=0,能不能推出b是零向量？3）对于实数a、b、c，有（a·b）·c=a·（b·c）但对于向量a，b，c来说，此式是否一定成立？解：a·b=|a||b|cosθ=5×4×cos120°=5×4×（-1/2）=－10。1）已知|a|=5，|b|=4，a与b的夹角θ=120°，求a·b。2）已知a=(1,1),b=(2,0),求a·b。解：|a|=√2,|b|=2,θ=45°∴a·b=|a||b|cosθ=√2×2×cos45°=2例1:物理上力所做的功实际上是将力正交分解，只有在位移方向上的力做功．θsFbOBaOA，作过点B作1BB1B垂直于直线OA，垂足为，则1OB|b|cosθOABab1BOABab)(1B|b|cosθ叫向量b在a方向上的投影．θ为锐角时，|b|cosθ＞0θ为钝角时，|b|cosθ＜0θ为直角时，|b|cosθ=0BOAab1B我们得到a·b的几何意义：数量积a·b等于a的长度|a|与b在a的方向上的投影|b|cosθ的乘积。例2、已知,4,6baab与的夹角为60°，求：（1）在方向上的投影；（2）在方向上的投影；bbaa||cosb=2cosa=33.平面向量的数量积的重要性质:a·b|a||b|（4）cosθ=（5）|a·b|≤|a||b|（3）当a与b同向时，a·b=|a||b|当a与b反向时，a·b=－|a||b|特别地，a·a=|a|2或|a|=√a·a。（2）aba·b=0⊥设a，b都是非零向量，e是与b方向相同的单位向量，θ是a与e的夹角，则（1）e·a=a·e=|a|cosθ1．若a=0，则对任一向量b，有a·b=02．若a≠0，则对任一非零向量b,有a·b≠03.若a≠0，a·b=0,则b=04.若a·b=0,则a·b中至少有一个为05.若a≠0，a·b=b·c,则a=c6.若a·b=a·c,则b≠c,当且仅当a=0时成立7.对任意向量a,b,c,有(a·b)·c≠a·(b·c)8.对任一向量a,有a2=|a|2练习：判断正误(√）(×）(×）(×）(×）(×）(×）(√）4、平面向量数量积的运算律已知向量和实数,则向量的数量积满足：,,abc（1）abba（交换律）（2）()()()ababab（数乘结合律）（3）()abcacbc（分配律）注意：数量积运算不满足结合律消去律5、平面向量数量积的常用公式2222))(1(bbaaba22))()(2(bababa求证：（1）（2）2222bbaaba22bababa证明：（1）2bababaaabaabbb222bbaa（2）bababaabbb22babaababbaababaa23120oabab已知，，与的夹角为，求练习4：）（））（；（）；（）（babababa3232122；）；（）（baba54解：3)21(32120cos1obaba）（22352323bbaababa）（））（（59422222baba）（223120cos52bbaao342715879642)(4222bbaababa）（199642)(5222bbaababa）（例3