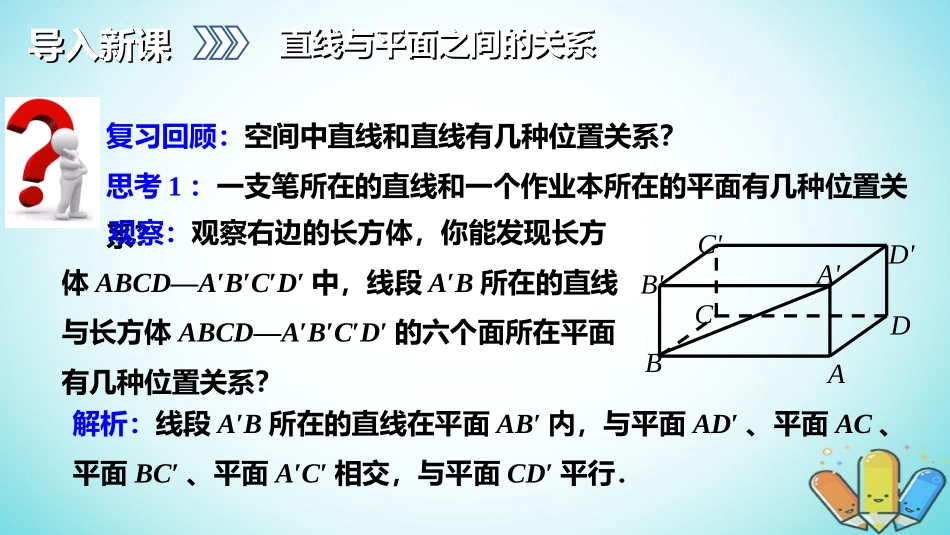
2.1.32.1.3空间中直线与平面之间的位置关系空间中直线与平面之间的位置关系三维目标三维目标空间中直线与平面之间的位置关系空间中直线与平面之间的位置关系1.知识与技能(1)结合图形正确理解空间中直线与平面之间的位置关系;2.过程与方法进一步熟悉文字语言、图形语言、符号语言的相互转换.3.情感、态度与价值观进一步培养学生的空间想象能力,以及有根有据、实事求是的科学态度和品质.学习目标导入新课导入新课直线与平面之间的关系直线与平面之间的关系复习回顾:空间中直线和直线有几种位置关系?思考1:一支笔所在的直线和一个作业本所在的平面有几种位置关系?观察:观察右边的长方体,你能发现长方体ABCD—A′B′C′D′中,线段A′B所在的直线与长方体ABCD—A′B′C′D′的六个面所在平面有几种位置关系?BADCA'B'D'C'解析:线段A′B所在的直线在平面AB′内,与平面AD′、平面AC、平面BC′、平面A′C′相交,与平面CD′平行.新课讲授新课讲授直线与平面的位置关系直线与平面的位置关系空间的直线与平面有如下三种位置关系:(1)直线在平面内——直线与平面有_______________________;(2)直线与平面相交——直线与平面________________________________;(3)直线与平面平行——直线与平面_____________________;(其中直线与平面相交或平行的情况统称为直线在平面外)[思考]直线a与平面α平行,直线b⊂α,则a与b有怎样的位置关系?无数个公共点有且只有一个公共点没有公共点解:由直线a与平面α平行,直线b⊂α知a与b没有公共点,所以a与b平行或异面.,记作a∥α,记作a⊂α,记作a∩α=A新课讲授新课讲授直线与平面的位置关系直线与平面的位置关系直线与平面αa直线与平面α相交αAaaα直线与平面α平行无交点直线在平面α内有无数个公共点有且只有一个交点典例精讲典例精讲直线与平面的位置关系直线与平面的位置关系例题精讲若一直线上有一点在已知平面外,则下列命题正确的是()A.直线上所有的点都在平面外B.直线上有无数多个点都在平面外C.直线上有无数多个点都在平面内D.直线上至少有一个点在平面内[解析]直线上有一点在平面外,则直线不在平面内,直线上有无数多个点在平面外.B一条直线l上有相异三个点A,B,C到平面α的距离相等,那么直线l与平面α的位置关系是()A.l∥αB.l⊥αC.l与α相交但不垂直D.l∥α或l⊂α典例精讲典例精讲直线与平面的位置关系直线与平面的位置关系[解析]l∥α时,直线l上任意点到α的距离都相等;l⊂α时,直线l上所有的点到α的距离都是0;l⊥α时,直线l上有两个点到α距离相等;l与α斜交时,也只能有两点到α距离相等.例题精讲D1.判断下列四个命题的对错.(1)若直线l上有无数个点不在平面α内,则l∥α.(2)若直线l与平面α平行,则l与平面α内的任意一条直线都平行.(3)若直线l与平面α平行,则l与平面α内的任意一条直线都没有公共点.(4)若两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行.达标训练知识识记知识识记直线与平面的位置关系直线与平面的位置关系(×)(×)(×)()知识识记知识识记(A)0个(B)1个(C)2个(D)3个AA达标训练直线与平面的位置关系直线与平面的位置关系知识识记知识识记DC直线与平面的位置关系直线与平面的位置关系知识识记知识识记(4).已知m,n为异面直线,m∥平面a,n∥平面b,a∩b=l,则l()(A)与m,n都相交(B)与m,n中至少一条相交(C)与m,n都不相交(D)与m,n中一条相交CC达标训练直线与平面的位置关系直线与平面的位置关系3.如图,直线a∥平面α,a⊂β,α∩β=b,求证:a∥b.证明:∵直线a∥平面α,∴直线a与平面α没有公共点.∵α∩β=b,∴b⊂α,b⊂β.∴直线a与b没有公共点.∵a⊂β,∴a∥b.知识识记知识识记直线与平面的位置关系直线与平面的位置关系课时小结:(师生互动,共同归纳)(1)本节课我们学习了哪些知识内容?(2)三个公理的内容及作用是什么?课堂小结课堂小结总结本节课的学习内容总结本节课的学习内容..课堂小结