高中数学 312指数函数(2)课件 苏教版必修1 课件VIP免费

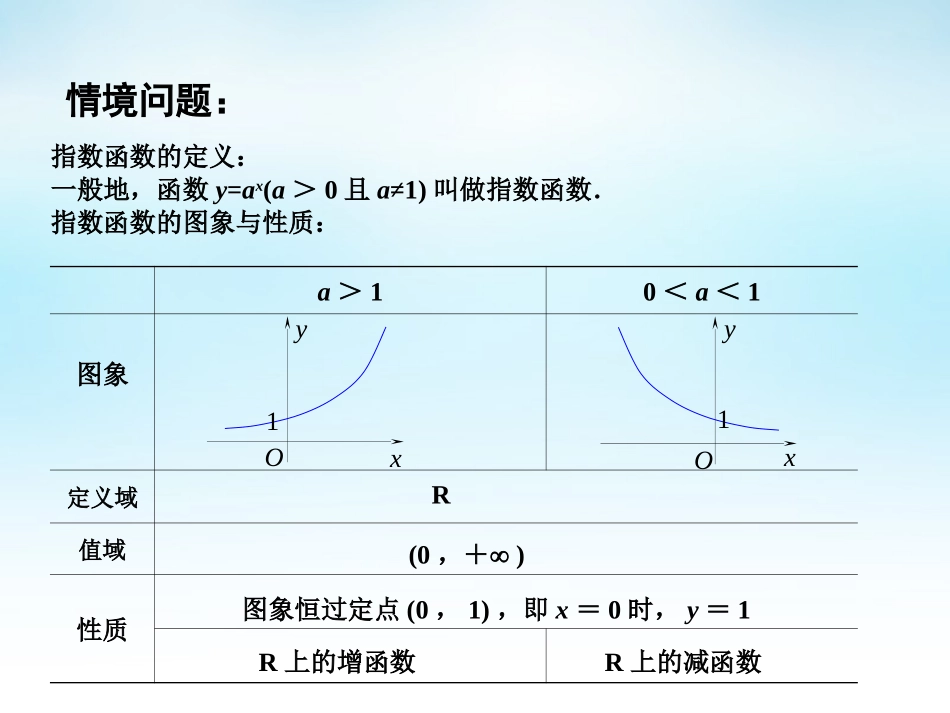
高中数学必修高中数学必修１１高中数学必修高中数学必修１１情境问题：一般地，函数y=ax(a＞0且a≠1)叫做指数函数．指数函数的定义：指数函数的图象与性质：a＞10＜a＜1图象定义域值域性质R(0，＋)xyO1R上的减函数xyO1图象恒过定点(0，1)，即x＝0时，y＝1R上的增函数情境问题：对于函数y＝ax(a＞0且a≠1)，图象恒过定点(0，1)．若a＞1，则当x＞0时，y1；而当x＜0时，y1；若0＜a＜1，则当x＞0时，y1；而当x＜0时，y1．数学应用：(1)3x≥1；(2)0.2x＜1；(3)3x≥30.5；(4)0.2x＜25；(5)9x＞3x-2；(6)3×4x－2×6x≤0．例1．解下列不等式：数学建构：例2．说明下列函数的图象与指数函数y=2x的图象的关系，并画出它们的示意图：(1)y=2x－2(2)y=2x＋2(3)y=2x－2(4)y=2x＋2注：(1)函数图象进行平移变换的一般规律：左右平移：y＝f(x)y＝f(x＋k)(当k＞0时，向左平移，反之向右平移)；上下平移：y＝f(x)y＝f(x)＋h(当h＞0时，向上平移，反之向下平移)．(2)如函数的图象有渐近线，平移时，渐近线应和图象一起平移．数学应用：(1)将函数f(x)＝3x的图象向右平移3个单位，再向下平移2个单位，可以得到函数的图象．(2)将函数f(x)＝3x的图象向右平移2个单位，再向上平移3个单位，可以得到函数的图象．(3)将函数f(x)＝＋2图象先向左平移2个单位，再向下平移1个单位所得函数的解析式是．(4)对任意的a＞0且a≠1，函数y＝a2x1的图象恒过的定点为，函数y＝a2x－1的图象恒过的定点的坐标是．213x数学探究：注：(1)函数图象对称变换的一般规律：完全变换：关于y轴对称y＝f(x)y＝f(－x)；关于x轴对称y＝f(x)y＝－f(x)．不完全变换：典型的有y＝f(x)y＝f(|x|)与y＝f(x)y＝|f(x)|．(2)函数的图象如有渐近线，对称变换时，渐近线应和图象一起翻折．(6)如何利用函数f(x)＝2x的图象，作出函数|f(x)－1|的图象？(5)如何利用函数f(x)＝2x的图象，作出函数y＝2|x|和y＝2|x－2|的图象？数学建构：平移变换：对称变换：完全对称变换：1．函数y＝f(x)的图象与函数y＝－f(x)的图象关于x轴对称；2．函数y＝f(x)的图象与函数y＝f(－x)的图象关于y轴对称；3．函数y＝f(x)的图象与到函数y＝－f(－x)的图象关于原点对称．1．函数y＝f(x)的图象与函数y＝f(x＋a)的图象关系为左右平移；2．函数y＝f(x)的图象与函数y＝f(x)＋a的图象关系为上下平移；局部对称变换：1．y＝|f(x)|的图象是保留函数y＝f(x)的图象上位于x轴上方部分，而将位于x轴下方部分作关于x轴对称变换；2．函数y＝f(|x|)的图象是保留y＝f(x)的图象上位于y轴右侧部分，而将位于y轴右侧部分作关于y轴对称变换；注：任一偶函数y＝f(x)都可以表示为y＝f(|x|)形式．数学应用：例3．已知函数y＝f(x)是定义在R上的奇函数，且x＜0时，f(x)＝1－2x，试画出此函数的图象．数学应用：例4．求函数的最小值以及取得最小值时的x值．1421xxy数学应用：(1)函数y＝ax在[0，1]上的最大值与最小值的和为3，则a等于．(2)函数y＝2|x|的值域为．(3)设a＞0且a≠1，如果y＝a2x＋2ax－1在[－1，1]上的最大值为14，求a的值．(4)当x＞0时，函数f(x)＝(a2－1)x的值总大于1，求实数a的取值范围．小结：1．指数函数的性质及应用；2．指数型函数的定点问题；3．指数型函数的草图及其变换规律．作业：P71第11，12，15题．数学探究：(2)对于任意的x1，x2R，若函数f(x)＝2x，试比较2f(x1)＋f(x2)与122xxf的大小．(1)函数f(x)的定义域为(0，1)，则函数的定义域为．222xxf