高三数学三角函数图象课件VIP免费

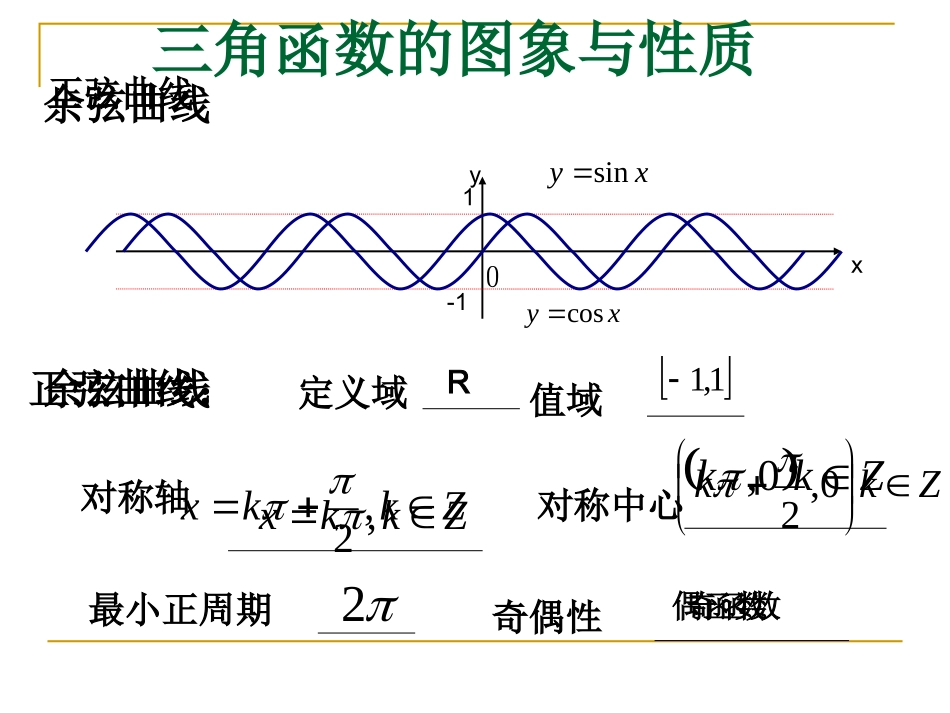
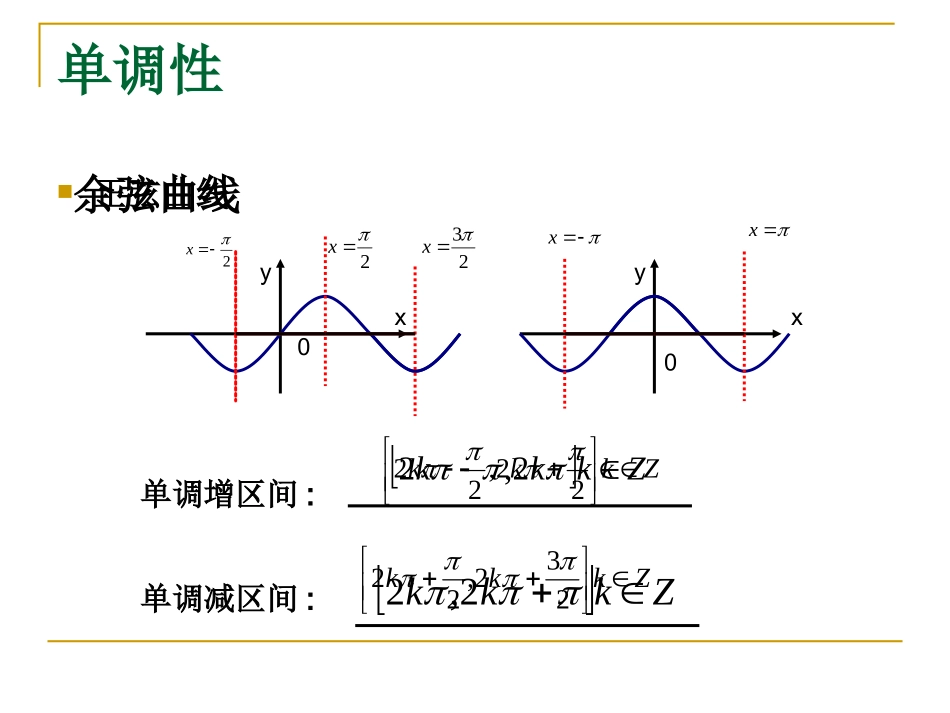
1五点作图法.三角函数的图象与性质2三角函数的图象画法3三角函数相关性质三角函数的图象与性质正弦曲线xy０1余弦曲线-1正弦曲线：xysinxycos最小正周期定义域值域对称轴对称中心R1,1Zkkx,2Zkk0,2奇偶性奇函数偶函数余弦曲线Zkkx,Zkk0,2单调性正弦曲线2x余弦曲线00xyyx2x23xxx单调增区间:单调减区间:Zkkk22,22Zkkk232,22Zkkk2,2Zkkk2,2正切曲线图象xy0232223分别从：定义域，值域，周期性，奇偶性，单调性，对称中心说明正切函数性质考点一五点作图法１已知函数.32sin2xy(１)用五点法作出函数的简图32x1226002232x.32sin2xy312765020xy06365127并指出函数的振幅,周期,初相,频率,单调区间五点作图法应用1若函数的图象如右，则xysin216xy01-13322.(06安徽)的图象按向量将函数)0(sinxy平移，)0,6(a平移后的图象如右图所示,则平移后的图象所对应的函数解析式是())6sin()(xyA)6sin()(xyB)32sin()(xyC)32sin()(xyDxy0-11127C例题分析例1已知RxAxAxf,0,0sin)(在一个周期内图象如图,求其解析式xy02-222232527答案:421sin2)(xxf练习与巩固练1如图是函数图象，则2sin2xy()6,1110.A6,1110.B6,2.C6,2.Dxy0121211练2(06四川)下列函数图象一部分如图则())6sin(.xyA)62sin(.xyB)34sin(.xyC)62sin(.xyDxy01126DC图象变换xysin个单位轴左移沿3x1说出下列变换的过程xy2sin横标缩小到原来的1/2(1)(2)xysinxysin2纵标扩大到原来的2倍(3)xysin)3sin(xy(4)xysin)32sin(xy个单位再沿轴向右平移的先将横坐标缩小到原来621xysin的解析式的图象相同，求恰好与函数)()6sin(3xfxy个单位，的图象右移先将函数8)(xfy)3sin(xyxy2sin)32sin(xy变式例2再把图象上每一点的横坐标扩大为原来的两倍,所得图象答案:)1252sin(3)(xxf链接高考的图象向左平移个单位,再向上平移1个单位,所得图象的函数解析式是sin2yx41(2009山东卷理)将函数sin2()4yx+13cos(2)yx4(,0)32（2009全国卷Ⅰ文）如果函数中心对称，那么的最小值为的图像关于点6解:cos2yx＝3＋43，04232k13()6kkZmin||6函数的图像关于点中心对称由此易得sin()yAx,,A0,0A[,0]3（2009江苏卷）函数（为常数，）在闭区间上的图象如图所示，则=.32T23T3，所以析34（2009宁夏海南卷理）已知函数y=sin（x+)(>0,-<)的图像如图所示，则=________________544,,2,125589,510Tx把代入y=sin有：1=sin109()2sin()fxx712f5（2009宁夏海南卷文）已知函数的图像如图所示，则。0