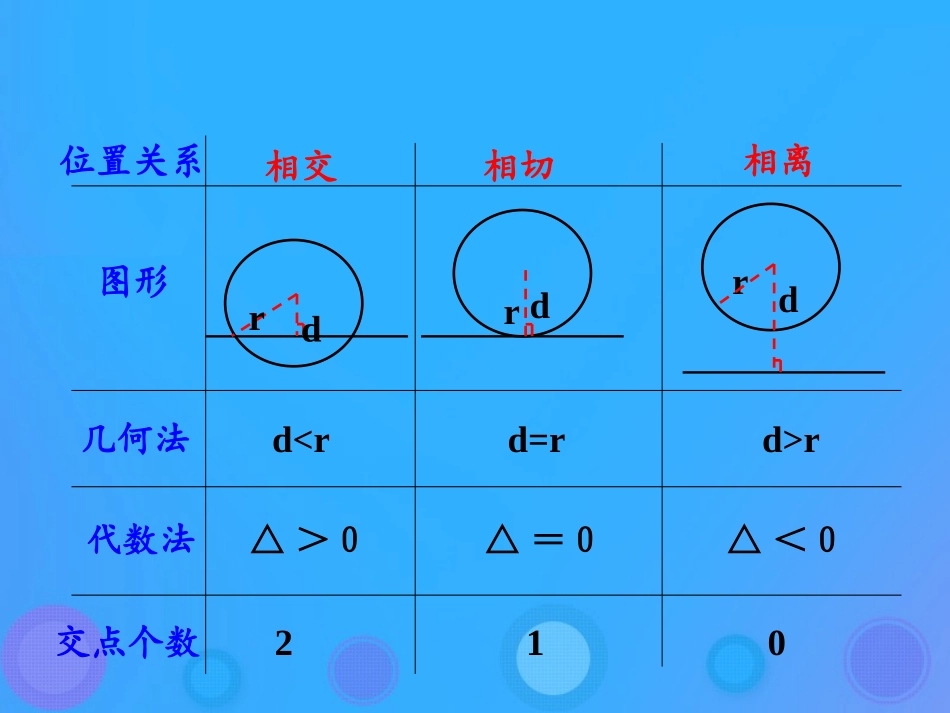
2.3.4圆与圆的位置关系直线与圆的位置关系的判定dddrrr几何法位置关系相交相切相离dr代数法交点个数△=0△>0△<0210图形外离d>R+rRrd圆与圆的位置关系有哪些?思考Rdr外切d=R+rRdr相交R-rr)Rd内切d=R-r(R>r)d内含dr)外离d>R+r外切d=R+r相交R-rr)内切d=R-r(R>r)内含dr)随着圆心距的增加,两圆的关系发生变化.思考已知两圆C1:x2+y2+D1x+E1y+F1=0和C2:x2+y2+D2x+E2y+F2=0,如何根据圆的方程判断圆与圆的位置关系?1.将两圆的方程化为标准方程;2.求两圆的圆心坐标和半径R、r;3.求两圆的圆心距d;4.比较d与R-r,R+r的大小关系.若d<|R-r|,则两圆内含;若d=|R-r|,则两圆内切;若|R-r|<d<R+r,则两圆相交;若d=R+r,则两圆外切;若d>R+r,则两圆外离.能否根据两个圆的公共点个数判断两圆的位置关系?思考•O1R•O2rd•O1R•O2rd•O1R•O2rd•O2rd•O1R•Rd•O2rO1两个圆相离△<0n=1两个圆相切△=0n=2两个圆相交△>0n=0利用两个圆的方程组成方程组的实数解的个数:的解的个数为n设方程组22222122rd)(yc)(xrb)(ya)(x几何法两圆的位置关系代数法d>r1+r2⇔相离⇒__________d=r1+r2⇔外切⇒Δ=0|r1-r2|<d<r1+r2⇔相交⇒________d=|r1-r2|⇔内切⇒_________d<|r1-r2|⇔内含⇒_________Δ<0Δ>0Δ=0Δ<0圆与圆的位置关系dRr两圆的位置关系公共点个数公切线条数几何法代数法相离00d>r1+r2Δ<0外切13d=r1+r2Δ=0相交22|r1-r2|<d<r1+r2Δ>0内切11d=|r1-r2|Δ=0内含00d<|r1-r2|Δ<0圆与圆的位置关032xyx08y6xyx2222解:将两圆方程联立:已知圆C1:x2+y2-6x+8y=0和圆C2:x2+y2+2x-3=0,试判断圆C1与圆C2的位置关系.例1方法一圆相交.所以有两个解,即:两其判别式为个圆的方程有:代入第两式相减得:0(-183)1284(80)Δ018380x128x038y8x22二方法二将C1的方程化成标准方程,得254)(y3)(x22将C2的方程化成标准方程,得4y1)(x22圆心坐标(3,-4),半径为5.圆心坐标(-1,0),半径为2.圆C1与C2的连心线的长为:240)4(1)(322圆C1与圆C2的半径长之和为:r1+r2=5+2=7圆C1与圆C2的半径长之差为:r1-r2=5-2=37243因为所以两圆相交.例2.a何值时,两圆:C1:x2+y2-2ax+4y+a2-5=0C2:x2+y2+2x-2ay+a2-3=0,(1)相切;(2)相交;(3)相离.2,),1(,4)()1(:3,),2,(,9)2()(:22221221raBayxCraAyaxC半径圆心半径圆心由已知得解:21||)1(rrAB当.,25两圆外切时或a23)2()1(22aa即||||21rrAB当23)2()1(22aa即.12时两圆内切或a2121||||)2(rrABrr当5)2()1(122aa即5212.aa或时两圆相交21||)3(rrAB当5)2()1(22aa即时两圆相离或25aa222212(1):230,:4230CxyxCxyxy222212(2):20,:2360CxyyCxyx22221(4)()25xyxya和a0,25,25aaa222223.(,)|4,(,)|(1)(1)(0),______________MxyxyNxyxyrrMNNr设集合当,则的取值范围是小试牛刀(一)2.两圆相切,试确定常数的值。1.判断下列两个圆的位置关系:022.r≤3.圆系与圆系方程具有某种共同性质的圆的集合,称为_______.(1)同心圆系(x-x0)2+(y-y0)2=r2,x0,y0为常数,r为参数.(2)圆心共线且半径相等圆系(x-x0)2+(y-y0)2=r2,r为常数,圆心(x0,y0)在直线Ax+By+C=0上移动.(3)过两已知圆x2+y2+D1x+E1y+F1=0,的交点的圆系方程:x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0,圆系222220xyDxEyF即f1(x,y)+λf2(x,y)=0(λ≠-1).当λ=-1时,变为(D1-D2)x+(E1-E2)y+F1-F2=0,表示过两圆的交点的直线(当两圆是同心圆时,此直线不存在),当两圆相交时,此直线为公共弦所在直线;当两圆相切时,此直线为两圆的公切线;当两圆相离时,此直线为与两圆连心线垂直的直线.(4)过直线与圆交点的圆系方程设直线l:Ax+By+C=0与圆C...