高中数学 4.2.3函数建模案例课件 北师大版必修1 课件VIP免费

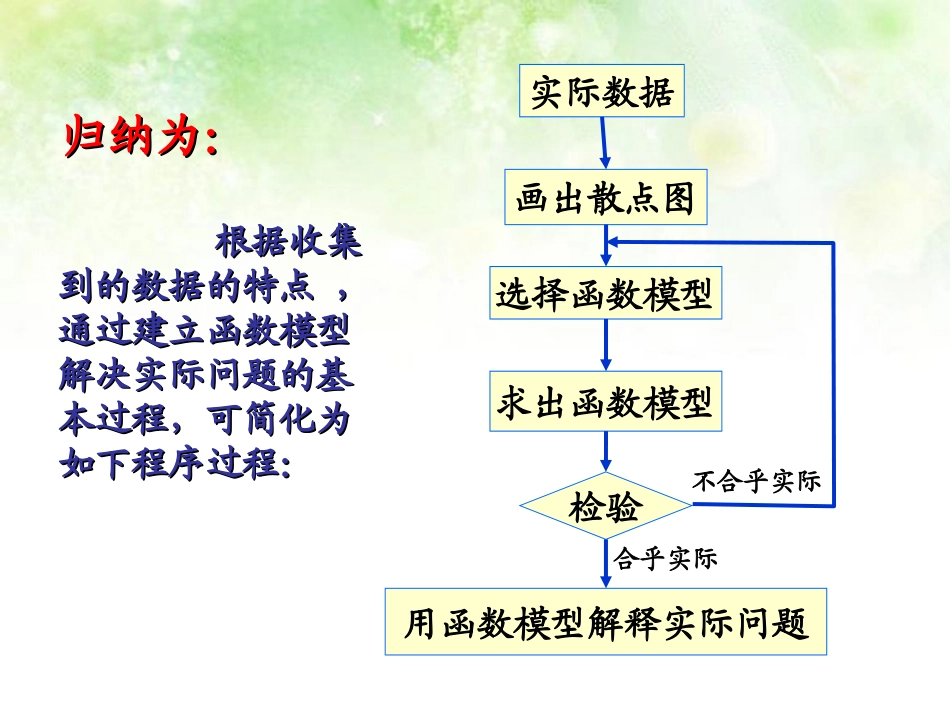
通过一些数据寻求事物规律，往往是通过绘出这些数据在直角坐标系中的点，观察这些点的整体特征，看它们接近我们熟悉的哪一种函数图像，选定函数形式后，将一些数据代入这个函数的一般表达式，求出具体的函数表达式，再做必要的检验，基本符合实际，就可以确定这个函数基本反映了事物规律，这种方法称为数据拟合.在自然科学和社会科学中，很多规律、定律都是先通过实验，得到数据，再通过数据拟合得到的。实际数据画出散点图选择函数模型求出函数模型检验用函数模型解释实际问题不合乎实际合乎实际归纳为：归纳为：根据收集根据收集到的数据的特点，到的数据的特点，通过建立函数模型通过建立函数模型解决实际问题的基解决实际问题的基本过程，可简化为本过程，可简化为如下程序过程：如下程序过程：例1.某地区不同身高的未成年男性的体重平均值如下表：身高/cm60708090100110体重/kg6.137.909.9912.1515.0217.50身高/cm120130140150160170体重/kg20.9226.8631.1138.8547.2555.05(1)根据表提供的的数据,能否建立一个恰当的函数模型,使它能近似地反映这个地区一体化未成年男性体重y㎏与身高x㎝的函数关系?试写出这个函数模型的关系式；解：(1)以身高为横坐标,体重为纵坐标,画出散点图010203040506060708090100110120130140150160170180根据图的分布特点,设y=a·bx这一函数来近似刻画其关系;取两点(70,7.90),(160,47.25),代入y=a·bx得：用计算器得：a2,b1.02这样就得到函数模型：y=21.02x16070.25.47.9.7baba解(2)将x=175代入y=21.02x，得y=21.02175用计算器得：y63.98由于7863.981.22>1.2,所以这个男生偏胖。(2)若体重超过相同身高男性体重的平均值的1.2倍为偏胖,低于0.8倍为偏瘦,那么这个地区一名身高为175㎝,体重为78㎏的在校男生的体重是否正常?例2已知某商品的价格每上涨x%,销售的数量就减少kx%,其中k为正常数.当时，该商品的价格上涨多少，就能使销售的总金额最大？21k解：1.设商品现定价a元,卖出数量为b个.由题设：当价格上涨x%时,销售总额为%)1(%)1(kxbxay]10000)1(100[100002xkkxaby得取21k]22500)50([200002xaby当x=50时，即该商品的价格上涨50%时，销售总金额最大。aby89max这个函数的图像如下图所示：解(1)阴影部分的面积为阴影部分的面积表示汽车在这5小时内行驶的路程为360km360165175190180150(2)根据图形可得：S200450t10t2054)1(80t21t2134)2(90t32t2224)3(75t43t2299)4(65t54t3.一辆汽车在某段路程中的行驶速度与时间的关系如图所示：（1）求图中阴影部分的面积，并说明所求面积的实际含义；（2）假设这辆汽车的里程表在汽车行驶这段路程前的读数为2004km，试建立汽车行驶这段路程时汽车里程表读数skm与时间th的函数解析式，并作出相应的图象908070605040302010vt123454.下图中哪几个图像与下述三件事分别吻合得最好？请你为剩下的那个图像写出一件事。①我离开家不久，发现自己把作业忘在家里，于是返回家里找到作业再上学②我骑车一路匀速行驶，只是在途中遇到一次交通堵塞，耽搁了一些时间③我出发后，心情轻松，缓慢行进，后来为了赶时间开始加速ABC0离家距离时间0离家距离时间0时间离家距离离家距离0时间DC.对应的参考事件：我出发后感到时间较紧，所以加速前进，后来发现时间还很充裕，于是放慢了速度.()()()DAB例5某桶装水经营部每天的房租、人员工资等固定成本为200元，每桶水的进价是5元，销售单价与日均销售量的关系如表所示：销售单价/元日均销售量/桶6789101112480440400360320280240请根据以上数据作出分析，这个经营部怎样定价才能获得最大利润？分析：由表中信息可知①销售单价每增加1元，日均销售量就减少40桶②销售利润怎样计算较好？解：设在进价基础上增加x元后，日均经营利润为y元，则有日均销售量为xx40520)1(40480（桶）而130,040520,0xxx即且1490)5.6(4020052040200)40520(22xxxxxyyx时，当5.6有最大值只需将销售单价定为11.5元，就可获得...