高中数学 三角函数的图象课件 北师大版必修4 课件VIP免费

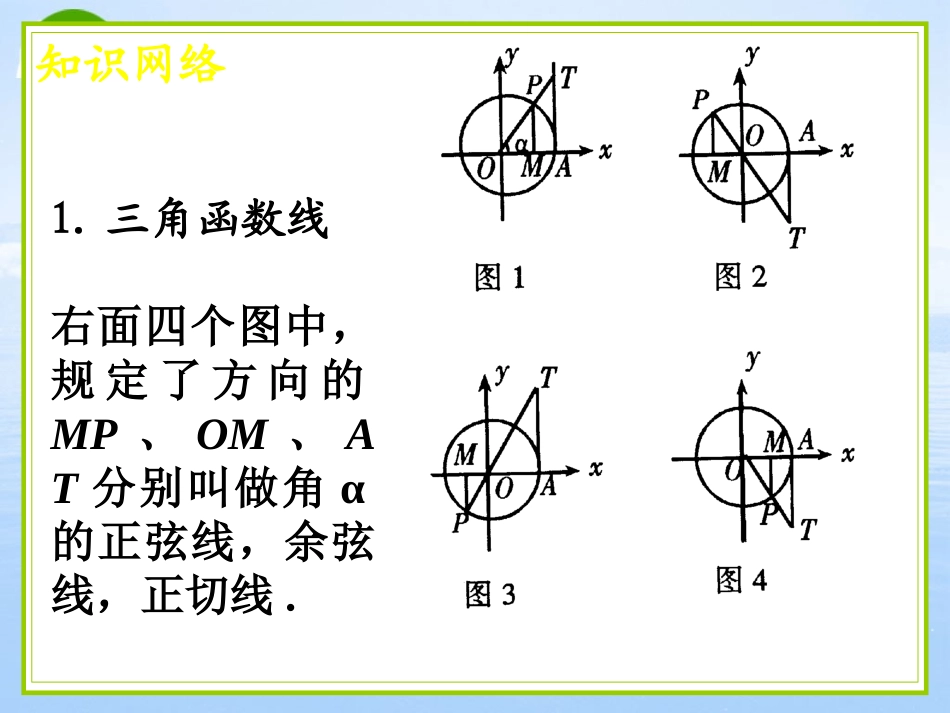
§4.6三角函数的图象知识网络1.三角函数线右面四个图中，规定了方向的MP、OM、AT分别叫做角α的正弦线，余弦线，正切线.知识网络2.三角函数的图象(1)y=sinx、y=cosx、y=tanx、y=cotx的图象(略)(2)y=Asin(ωx+φ)的图象及作法知识网络(3)三角函数的图象变换①振幅变换：y=sinx→y=Asinx将y=sinx的图象上各点的纵坐标变为原来的A倍(横坐标不变)；②相位变换：y=Asinx→y=Asin(x+φ)将y=Asinx的图象上所有点向左(φ＞0)或向右(φ＜0)平移|φ|个单位；③周期变换：y=Asin(x+φ)→y=Asin(ωx+φ)将y=Asin(x+φ)图象上各点的横坐标变为原来的1/ω倍(纵坐标不变).知识网络3.图象的对称性函数y=Asin(ωx+φ)(A＞0，ω＞0)的图象具有轴对称和中心对称.具体如下：(1)函数y=Asin(ωx+φ)的图象关于直线x=xk(其中ωxk+φ=kπ+π/2，kZ)∈成轴对称图形.(2)函数y=Asin(ωx+φ)的图象关于点(xj,0)(其中ωxj+φ=kπ,kZ)∈成中心对称图形.重庆市万州高级中学曾国荣wzzxzgr@126.com知识网络4、一般函数图象变换基本变换平移变换伸缩变换上下平移左右平移上下伸缩左右伸缩y=f(x)图象y=f(x)+b图象y=f(x+φ)图象y=Af(x)图象y=f(ωx)图象向上(b>0)或向下(b<0)移︱b︱单位向左(φ>0)或向右(φ<0)移︱φ︱单位点的横坐标变为原来的1/ω倍纵坐标不变点的纵坐标变为原来的A倍横坐标不变复习导引1、请分别作出当的终边在第一、二、三、四象限时的正弦线、余弦线、正切线，并思考如何作出余切线？2、你能否非常熟练地画出正弦函数、余弦函数、正切函数、余切函数在原点附近两个周期内的图象？3、在图象变换过程中，先相位变换后周期变换与先周期变换后相位变换有什么区别和联系？4、已知y=Asin(ωx+)的一段图象，确定A、ω、的一般方法是什么？考点练习A1.(20013sin()23.43.43.3.3xyABCD年天津）函数的周期、振幅依次是（）、、、、考点练习D2.cosyxx函数的部分图象是图中的（）OxyOxyOxyOxyABCDC4sin()3yx3、把函数的图象向右平移个单位，所得图象正好关于原点对称，则的最小正值为()A、B、C、D、6432考点练习B4、若函数y=cosx的图象上的点纵坐标不变，将横坐标缩小为原来的，再将所得图象沿x轴向左平移个单位，则新图象对应的函数式是()A、B、C、D、)32cos(xy2cos(4)3yx2sin(4)3yxsin(2)3yx614考点练习30424、、、、5、用五点法作的图象时，首先应描出的五点的横坐标可以是.3sin2yx考点练习右6、要得到的图象，只需将的图象向平移个单位.cos()24xycos2xy2典型题选讲【例1】要得到函数y=3cos(2x－)的图象，可以将函数y=3sin2x的图象()A、沿x轴向左平移个单位B、沿x轴向右平移个单位C、沿x轴向左平移个单位D、沿x轴向右平移个单位48844典型题选讲解析：此题为选择题，可采用逐个尝试的方法作出，如果作为填空题或解答题，可采用待定系数法求之。即设所以由本题选项的特殊性可令因此，故选A。3sin2()3cos(2)4xxsin(22)cos(2)sin(2)244xxx2224xx8典型题选讲Ox21–1–2y【例2】已知下图是函数的图象(1)求的值；(2)求函数图象的对称轴方程.sin()yAx、典型题选讲Ox21–1–2y解析：解这类问题的一般方法是通过特殊点来确定函数中的，于是由题设图象知:（1）（2）函数图象的对称轴方程为即。,,A2062sin(2)1162612yx2,62xk,()26kxkZ典型题选讲【例3】已知函数给出下列四个命题:(1)该函数的值域是[–1，1]；(2)当且仅当时，该函数取得最小值1；(3)该函数是以为最小正周期的周期函数；(4)当且仅当上述命题中正确的命题是.sin(sincos)()cos(sincos)xxxfxxxx)(22zkkx322,()2kxkkz()0fx时，。典型题选讲【例4】(1)试求函数的定义域；236lgcosyxx解析：求函数定义域实质就是求不等式组的解集，再利用三角函数图象求解。2cos0360xx2cos0360xxcos066xx3366.2222xx...