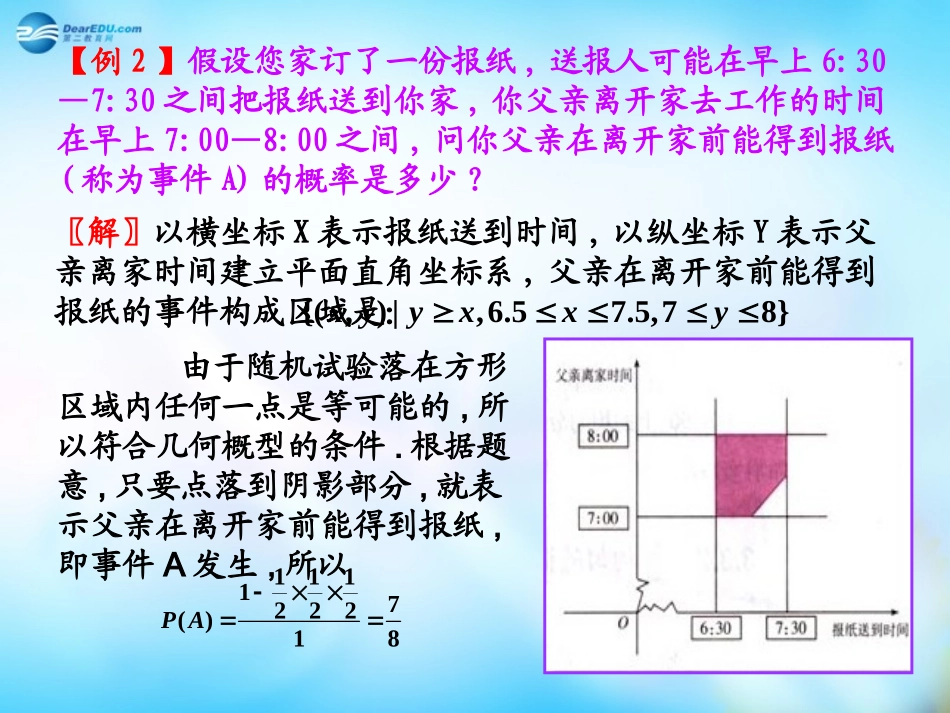
学习目标1.掌握利用计算机(计算器)产生均匀随机数的方法,并学会利用随机模拟方法估计未知量.2.通过例2理解随机模拟的基本思想是用频率估计概率.【例2】假设您家订了一份报纸,送报人可能在早上6:30—7:30之间把报纸送到你家,你父亲离开家去工作的时间在早上7:00—8:00之间,问你父亲在离开家前能得到报纸(称为事件A)的概率是多少?〖解〗以横坐标X表示报纸送到时间,以纵坐标Y表示父亲离家时间建立平面直角坐标系,父亲在离开家前能得到报纸的事件构成区域是:{(,)|,6.57.5,78}xyyxxy由于随机试验落在方形区域内任何一点是等可能的,所以符合几何概型的条件.根据题意,只要点落到阴影部分,就表示父亲在离开家前能得到报纸,即事件A发生,所以11117222()18PA方法2、(随机模拟的方法)我们可以用两个带有指针(分针)的圆盘,标上时间,分别旋转两个圆盘,记下父亲在离开家前能得到报纸的次数,则P(A)=父亲在离家前能得到报纸的次数/试验的总次数我们也可以用计算机产生随机数模拟试验,X是0-1之间的均匀随机数,Y也是0-1之间的均匀随机数,如果Y+7>X+6.5,即Y>X-0.5,那么父亲在离开家前能得到报纸。用计算机产生随机数模拟试验1.选定A1格,键入“=RAND()”,按Enter键,则在此格中的数是随机产生的[0,1]之间的均匀随机数.2.选定A1格,按Ctrl+C快捷键,选定A2~A50,B1~B50,按Ctrl+V快捷键,则在A2~A50,B1~B50的数均为[0,1]之间的均匀随机数.用A列的数加7表示父亲离开家的时间,B列的数加6.5表示报纸到达的时间.这样我们相当于做了50次随机试验.3.如果A+7>B+6.5,即A-B>-0.5,则表示父亲在离开家前能得到报纸.4.选定D1格,键入“=A1-B1”;再选定D1,按Ctrl+C,选定D2~D50,按Ctrl+V.5.选定E1格,键入频数函数“=FREQUENCY(D1:D50,-0.5)”,按Enter键,此数是统计D列中,比-0.5小的数的个数,即父亲在离开家前不能得到报纸的频数.6.选定F1格,键入“=1-E1/50”,按Enter键,此数是表示统计50次试验中,父亲在离开家前能得到报纸的频率.【例3】在正方形中随机撒一把豆子,用随机模拟的方法估计圆周率的值.豆子落在圆内的概率=圆的面积正方形的面积≈落在圆中的豆子数落在正方形中的豆子数圆的面积正方形的面积21224≈落在圆中的豆子数落在正方形中的豆子数4随着试验次数的增大,结果的精度会越来越高.用计算机产生随机数模拟试验1.选定A1,键入“=(rand()-0.5)*2”,表示得到[-1,1]之间的随机数.2.选定A1格,按Ctrl+C,选定A2~A1000,B1~B1000,按Ctrl+V,则在A2~A1000,B1~B1000的数均为[-1,1]之间的均匀随机数.3.选定D1,键入“=power(A1,2)+power(B1,2)”,再选定D1,按“ctrl+C”,选定D2~D1000,按“ctrl+V”,则D列表示A2+B2.4.选定F1,键入“=IF(D1>1,1,0)”,再选定F1,按“ctrl+C”,选定F2~F1000,按“ctrl+V”.则如果D列中A2+B2>1,F列中的值为1,否则F列中的值为0.5.选定H1,键入“=frequency(F1:F10,0.5)”,表示F1~F10中小于0.5的个数,即前10次试验中落在圆内的豆子数;类似地,分别得到表示前20次、50次、100次、500次、1000次试验中落在圆内的豆子数.6.选定I1,键入“=H1*4/10”,表示根据前10次试验得到圆周率的估计值,类似地,可以得到根据前20次、50次、100次、500次和1000次试验得到的圆周率的估计值.【例4】利用随机模拟方法计算图中阴影部分(y=1和y=x2所围成的部分)的面积.根据几何概型计算概率的公式,概率等于面积之比.如果概率用频率近似,在不规则图形外套上一个规则图形,则不规则图形的面积近似等于规则图形的面积乘以频率.而频率可以通过模拟的方法得到,从而得到了不规则图形面积的近似值.本题套上的规则图形面积为2,所以本题所求的不规则图形的面积等于频率乘以2.用计算机产生随机数模拟试验1.选定A1,键入“=(RAND()-0.5)*2”,表示得到[-1,1]之间的随机数.选定A1格,按Ctrl+C,选定A2~A1000,按Ctrl+V,则在A2~A1000的数均为[-1,1]之间的均匀随机数.2.选定B1,键入“=RAND()”,表示得到[0,1]之间的随机数.选定B1格,按Ctrl+C,选定B2~B1000,按Ctrl+V,则在B1~B1000的数均为[0...