高一数学 (143正切函数的性质与图象)课件VIP免费

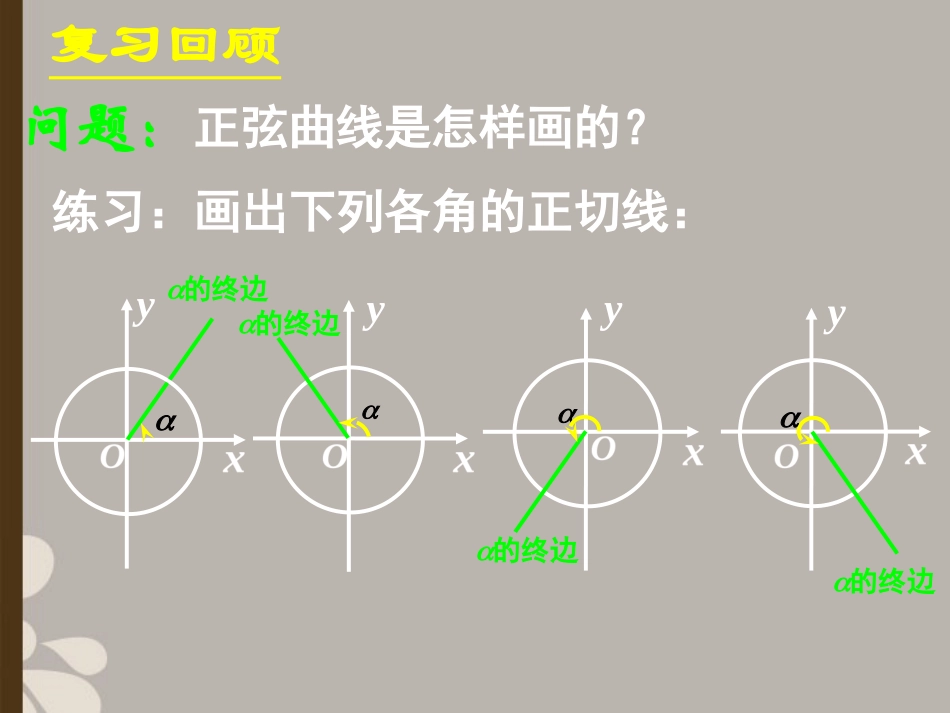
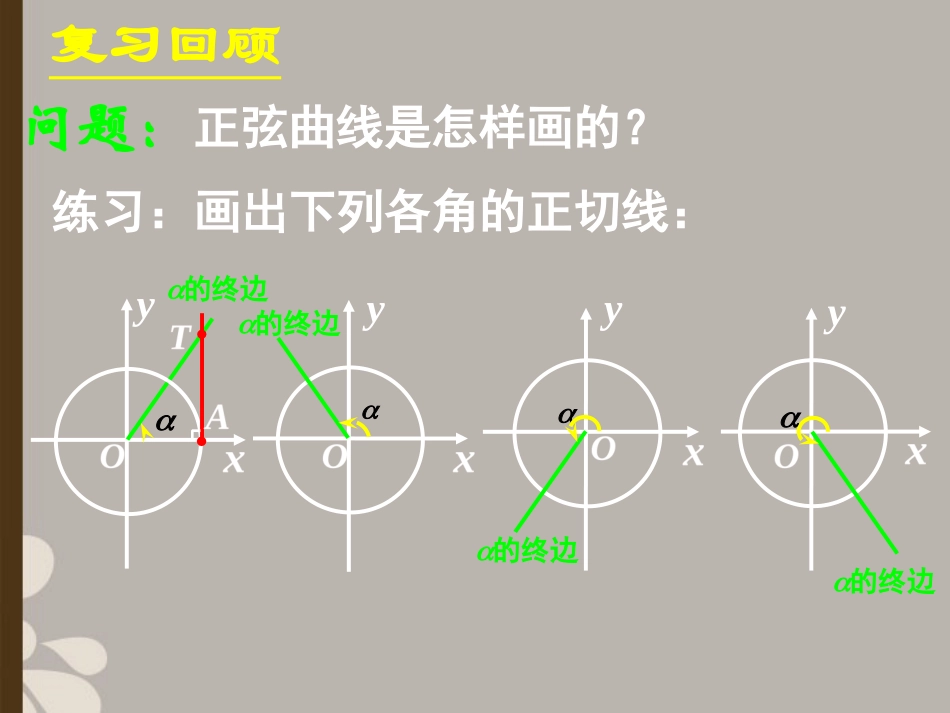
复习回顾问题：正弦曲线是怎样画的？练习：画出下列各角的正切线：的终边的终边的终边y的终边yyy复习回顾问题：正弦曲线是怎样画的？练习：画出下列各角的正切线：的终边的终边的终边y的终边yyy复习回顾问题：正弦曲线是怎样画的？练习：画出下列各角的正切线：的终边的终边的终边y的终边yyy复习回顾问题：正弦曲线是怎样画的？练习：画出下列各角的正切线：的终边的终边的终边y的终边yyy复习回顾问题：正弦曲线是怎样画的？练习：画出下列各角的正切线：的终边的终边的终边y的终边yyy讲授新课1.正切函数y=tanx的定义域是什么？思考：讲授新课1.正切函数y=tanx的定义域是什么？2.正切函数是不是周期函数？思考：讲授新课1.正切函数y=tanx的定义域是什么？2.正切函数是不是周期函数？3.正切函数是奇函数还是偶函数？思考：讲授新课1.正切函数y=tanx的定义域是什么？2.正切函数是不是周期函数？3.正切函数是奇函数还是偶函数？4.正切函数的单调性怎样？思考：讲授新课1.正切函数y=tanx的定义域是什么？2.正切函数是不是周期函数？3.正切函数是奇函数还是偶函数？4.正切函数的单调性怎样？5.正切函数的值域是什么？思考：讲授新课总结:正切函数的性质定义域值域周期奇偶性单调性讲授新课定义域}Z,2|{kkxx值域周期奇偶性单调性总结:正切函数的性质讲授新课定义域}Z,2|{kkxx值域R周期奇偶性单调性总结:正切函数的性质讲授新课定义域}Z,2|{kkxx值域R周期T奇偶性单调性总结:正切函数的性质讲授新课定义域}Z,2|{kkxx值域R周期T奇偶性奇函数,tan)tan(xx单调性总结:正切函数的性质讲授新课定义域}Z,2|{kkxx值域R周期T奇偶性奇函数,tan)tan(xx单调性内，函数单调递增在开区间Z)2,2(kkk总结:正切函数的性质讲授新课讲授新课xy22o6464讲授新课xy22o6464讲授新课xy22o6464讲授新课xy22o6464讲授新课xy22o6464讲授新课xy22o6464讲授新课xy22o6464讲授新课xy22o6464讲授新课xy22o6464讲授新课xy22o6464讲授新课xy22o6464讲授新课xy22o6464讲授新课xy22o6464讲授新课xy22o6464讲授新课(1)正切函数的最小正周期不能比小，正切函数的最小正周期是；说明:讲授新课(1)正切函数的最小正周期不能比小，正切函数的最小正周期是；(2)根据正切函数的周期性，把上述图象向左、右扩展，得到正切函数的图象，称“正切曲线”.说明:讲授新课Oxy讲授新课Oxy讲授新课Oxy讲授新课Oxy(3)正切曲线是由被相互平行的直线所隔开的无穷多支曲线组成的.讲授新课例1..517tan413tan的大小与比较讲授新课例2.求下列函数的周期：讲授新课例3.求函数33tanxy值域，指出它的周期性、单调性.的定义域、讲授新课例3.求函数33tanxy值域，指出它的周期性、单调性.的定义域、思考：你能判断它的奇偶性吗？讲授新课例3.求函数33tanxy值域，指出它的周期性、单调性.的定义域、思考：你能判断它的奇偶性吗？非奇非偶函数讲授新课练习1..32tan单调性域、周期性、奇偶性、的定义求函数xy讲授新课练习1..32tan单调性域、周期性、奇偶性、的定义求函数xy练习2.教材P.45第2、3、4、5、6题.讲授新课思考：你能用图象求函数tan3yx3tanxy的定义域吗?课堂小结1.正切函数的图象；2.正切函数的性质.课后作业1.阅读教材P.42-P.45；2.《习案》作业十一.