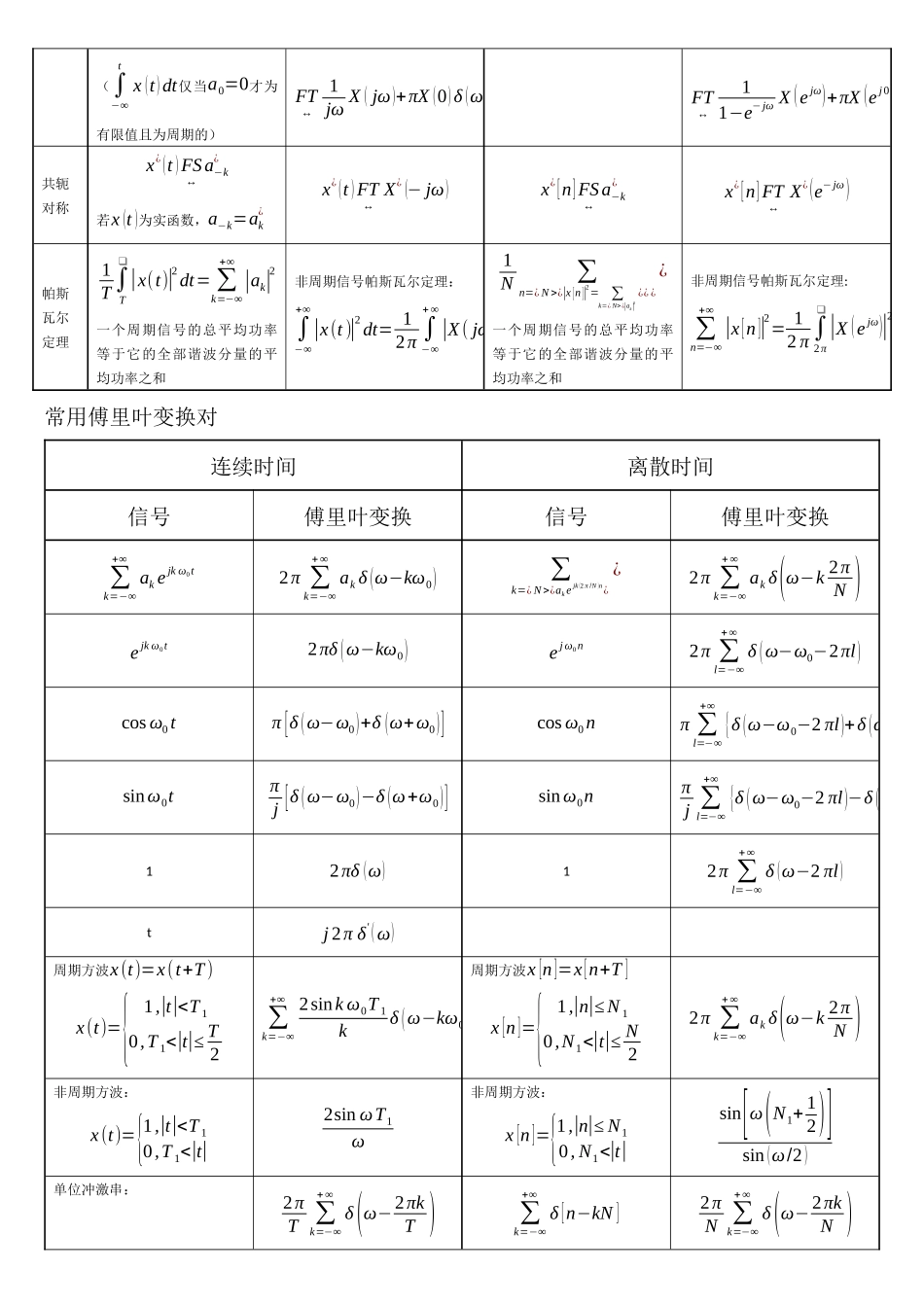
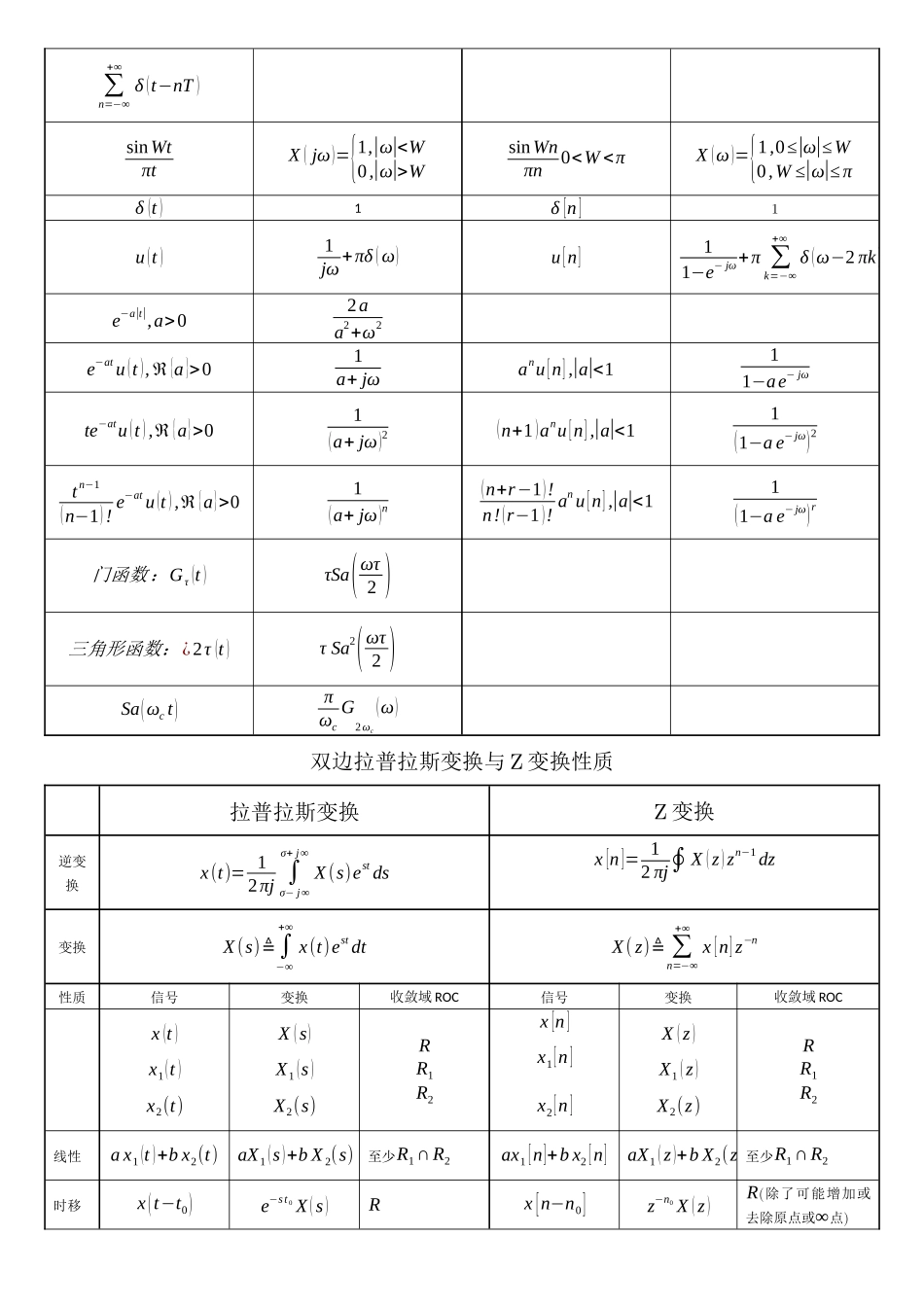
连续时间离散时间傅里叶级数FS傅里叶变换FT傅里叶级数FS傅里叶变换FT时域x(t)=∑k=−∞+∞akejkω0t连续时间,在时间上是周期的x(t)=12π∫−∞+∞X(jω)ejωtdω连续时间,在时间上是非周期的x[n]=∑k=¿N>¿akejk(2π/N)n¿¿离散时间,在时间上是周期的x[n]=12π∫2π❑X(ejω)ejωndω离散时间,在时间上是非周期的频域ak=1T∫T❑x(t)e−jkω0tdt离散频率,在频率上是非周期的X(jω)=∫−∞+∞x(t)e−jωtdt连续频率,在频率上是非周期的ak=1N∑n=¿N>¿x[n]e−jk(2π/N)n¿¿离散频率,在频率上是周期的X(ejω)=∑n=−∞+∞x[n]e−jωn连续频率,在频率上是周期的x(t)FS↔ak,y(t)FS↔bk,周期为T,基本频率ω0=2π/Tx(t)FT↔X(jω),y(t)FT↔Y(jω)若:x[n]FS↔ak,y[n]FS↔bk,周期为N,基本频率ω0=2π/N{x[n]y[n]FT⇒{X(ejω)Y(ejω)(频率周期为2π)线性性质Ax(t)+By(t)FS↔Aak+BbkAx(t)+By(t)FT↔AX(jω)+BY(jω)Ax[n]+By[n]FS↔Aak+BbkAx[n]+By[n]FT↔AX(ejω)+BY(ejω)时移性质x(t−t0)FS↔e−jkω0t0akx(t−t0)FT↔e−jωt0X(jω)x[n−n0]FS↔e−jkω0n0akx[n−n0]FT↔e−jωn0X(ejω)频移性质ejω0tx(t)FT↔X(j(ω−ω0))ejω0nx(t)FT↔X(ej(ω−ω0))对称X(jt)FT↔2πx(−ω)时间反转x(−t)FS↔a−kx(−t)FT↔X(−jω)x[−n]FS↔a−kx[−n]FT↔X(e−jω)时域变换x(αt)=∑k=−∞+∞akejk(αω¿¿0)tFS↔ak¿x(αt)FT↔1|α|X(jωα)x(m)[n]={x[n/m]若n是m整数倍0若n不是m的整数倍FS↔1mak(周期为mN)x(k)[n]={x[n/k]若n是k整数倍0若n不是k的整数倍FT↔X(ejkω)相乘x(t)y(t)FS↔∑l=−∞+∞albk−lx(t)y(t)FT↔12πX(jω)∗Y(jω)x[n]y[n]FS↔∑l=¿N>¿alak−l¿¿x[n]y[n]FT↔12πX(ejω)∗Y(ejω)卷积周期卷积:∫T❑x(τ)y(t−τ)dτFS↔Takbkx(t)∗y(t)FT↔X(jω)Y(jω)周期卷积:∑r=¿N>¿x[r]y[n−r]FS↔Nakbk¿¿x[n]∗y[n]FT↔X(ejω)Y(ejω)时域微分dx(t)dtFS↔jkω0ak=jk2πTakdx(t)dtFT↔jωX(jω)x[n]−x[n−1]FS↔(1−e−jk(2π/N))akx[n]−x[n−1]FT↔(1−e−jω)X(ejω)频域微分tx(t)FT↔jdX(jω)dωnx[n]FT↔jdX(ejω)dω积分∫−∞tx(t)dtFS↔(1jkω0)ak∫−∞tx(t)dt∑k=−∞nx[k]¿∑k=−∞nx[k](∫−∞tx(t)dt仅当a0=0才为有限值且为周期的)FT↔1jωX(jω)+πX(0)δ(ω)FT↔11−e−jωX(ejω)+πX(ej0)∑k=−∞+∞δ(ω−2πk)共轭对称x¿(t)FS↔a−k¿若x(t)为实函数,a−k=ak¿x¿(t)FT↔X¿(−jω)x¿[n]FS↔a−k¿x¿[n]FT↔X¿(e−jω)帕斯瓦尔定理1T∫T❑|x(t)|2dt=∑k=−∞+∞|ak|2一个周期信号的总平均功率等于它的全部谐波分量的平均功率之和非周期信号帕斯瓦尔定理:∫−∞+∞|x(t)|2dt=12π∫−∞+∞|X(jω)|2dω1N∑n=¿N>¿|x[n]|2=∑k=¿N>¿|ak|2¿¿¿¿一个周期信号的总平均功率等于它的全部谐波分量的平均功率之和非周期信号帕斯瓦尔定理:∑n=−∞+∞|x[n]|2=12π∫2π❑|X(ejω)|2dω常用傅里叶变换对连续时间离散时间信号傅里叶变换信号傅里叶变换∑k=−∞+∞akejkω0t2π∑k=−∞+∞akδ(ω−kω0)∑k=¿N>¿akejk(2π/N)n¿¿2π∑k=−∞+∞akδ(ω−k2πN)ejkω0t2πδ(ω−kω0)ejω0n2π∑l=−∞+∞δ(ω−ω0−2πl)cosω0tπ[δ(ω−ω0)+δ(ω+ω0)]cosω0nπ∑l=−∞+∞{δ(ω−ω0−2πl)+δ(ω+ω0−2πl)}sinω0tπj[δ(ω−ω0)−δ(ω+ω0)]sinω0nπj∑l=−∞+∞{δ(ω−ω0−2πl)−δ(ω+ω0−2πl)}12πδ(ω)12π∑l=−∞+∞δ(ω−2πl)tj2πδ'(ω)周期方波x(t)=x(t+T)x(t)={1,|t|WsinWnπn0