信号与系统复习题2VIP免费

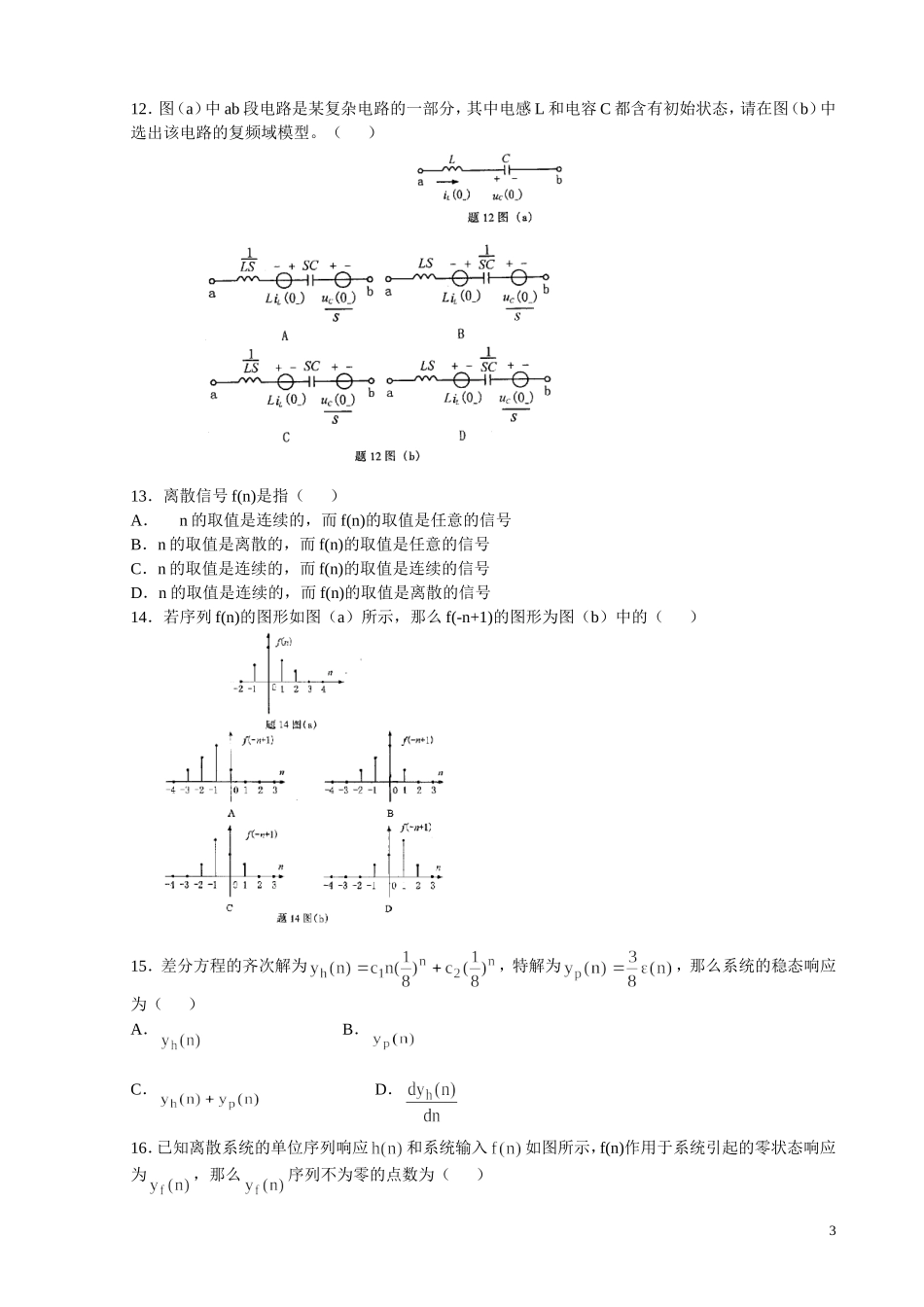
信号与系统复习题2第一部分选择题一、单项选择题2.积分式等于()A.1B.0C.-1D.-23.已知信号f(t)如题3(a)图所示，则f(-2t-2)为题3(b)图中的()4.已知一线性时不变系统在题4(a)图所示信号的激励下的零状态响应如题4(b)图所示，则在如题4(c)图所示信号的激励下的零状态响应为题4(d)图中的()5.题5图中f(t)是周期为T的周期信号，f(t)的三角函数形式的傅里叶级数系数的特点是()A.仅有正弦项B.既有正弦项和余弦项，又有直流项C.既有正弦项又有余弦项1D.仅有余弦项6.已知F(j)=，则F(j)所对应的时间函数为()A.B.C.D.7．信号和分别如图（a）和图(b)所示，已知，则的傅里叶变换为（）A．B．C．D．8.单边拉普拉斯变换F(S)=1+S的原函数f(t)=()。(A)e-t·ε(t)(B)(1+e-t)ε(t)(C)(t+1)ε(t)(D)δ(t)+δ′(t)9.如某一因果线性时不变系统的系统函数H(S)的所有极点的实部都小于零，则()。(A)系统为非稳定系统(B)|h(t)|<∞(C)系统为稳定系统(D)∫∞0|h(t)|·dt=010.离散线性时不变系统的单位序列响应h(n)为()(A)对输入为δ(n)的零状态响应(B)输入为ε(n)的响应(C)系统的自由响应(D)系统的强迫响应C．D．11．的拉氏反变换为（）A．B．C．D．212．图（a）中ab段电路是某复杂电路的一部分，其中电感L和电容C都含有初始状态，请在图（b）中选出该电路的复频域模型。（）13．离散信号f(n)是指（）A．n的取值是连续的，而f(n)的取值是任意的信号B．n的取值是离散的，而f(n)的取值是任意的信号C．n的取值是连续的，而f(n)的取值是连续的信号D．n的取值是连续的，而f(n)的取值是离散的信号14．若序列f(n)的图形如图（a）所示，那么f(-n+1)的图形为图（b）中的（）15．差分方程的齐次解为，特解为，那么系统的稳态响应为（）A．B．C．D．16．已知离散系统的单位序列响应和系统输入如图所示，f(n)作用于系统引起的零状态响应为，那么序列不为零的点数为（）3A．3个B．4个C．5个D．6个第二部分非选择题二、填空题17．=。18．GLC并联电路发生谐振时，电容上电流的幅值是电流源幅值的倍。19．在一个周期内绝对可积是周期信号频谱存在的条件。20．已知一周期信号的幅度谱和相位谱分别如图(a)和图(b)所示，则该周期信号f(t)=。21．如果已知系统的单位冲激响应为h(t)，则该系统函数H(s)为。22．H(s)的零点和极点中仅决定了h(t)的函数形式。23．单位序列响应h(n)是指离散系统的激励为时，系统的零状态响应。24．我们将使收敛的z取值范围称为。25．在变换域中解差分方程时，首先要对差分方程两端进行。三、计算题(本大题共10小题，每小题5分，共50分)26．如图示串联电路的谐振频率，电源电压mV，谐振时的电容电压有效值求谐振时的电流有效值I，并求元件参数L和回路的品质因数Q。427．已知信号f(2-t)的波形如图所示，绘出f(t)的波形。28．已知信号x(t)的傅里叶变换X(j)如图所示，求信息x(t)。29．如图所示电路，已知，求电路中消耗的平均功率P。30．求的拉氏变换。31．已知电路如图示，t=0以前开关位于“1”，电路已进入稳态,t=0时刻转至“2”，用拉氏变换法求电流i(t)的全响应。532．已知信号x(t)如图所示，利用微分或积分特性，计算其傅里叶变换。33．求的逆Z变换f(n)，并画出f(n)的图形（-4≤n≤6）。34．已知某线性时不变系统，f（t）为输入，y(t)为输出，系统的单位冲激响应。若输入信号，利用卷积积分求系统输出的零状态响应yf(t)。35．用拉氏变换法求解以下二阶系统的零输入响应yx(t)、零状态响应yf(t)及全响应y(t)。参考答案2一、单项选择题1.A2.C3.A4.C5.D6.B7.A8.D9.C10.A11.D12.B13.B14.D15.B16.C二、填空题17．18．Q19．必要20．21．[h(t)]22.极点623．单位序列或24．收敛域25．Z变换一、计算题26．I=5mA；L=5mH；Q=10027.28.由可以看出，这是一个调制信号的频谱，x(t)可以看作信号x1(t)与cos500t的乘积。由x1(t)的频谱为而x1(t)=所以x(t)=x1(t)cos500t=29．阻抗Z=R+jL=1+j则7或用微分性质做：31．伏开关到“2”之后的复频域模型为答31图32．令，则y(t)如图所示则=由于，根据时域积分特性33．8或35．方程两边拉氏变换得：910