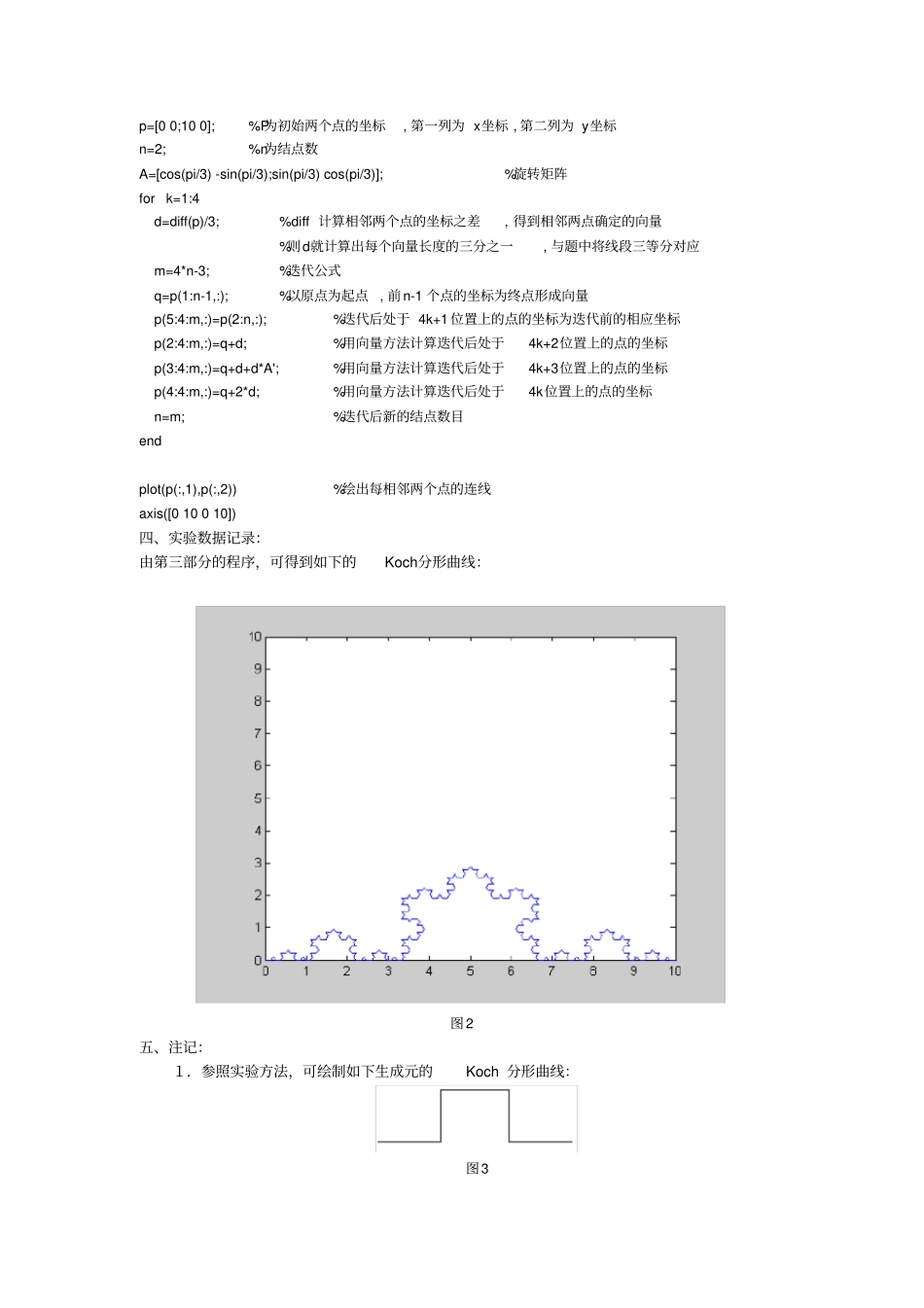
几个分形的 matlab实现摘要:给出几个分形的实例,并用matlab 编程实现方便更好的理解分形,欣赏其带来的数学美感关键字: Koch 曲线实验图像一、问题描述:从一条直线段开始,将线段中间的三分之一部分用一个等边三角形的两边代替,形成山丘形图形如下图1在新的图形中, 又将图中每一直线段中间的三分之一部分都用一个等边三角形的两条边代替,再次形成新的图形如此迭代,形成Koch分形曲线。二、算法分析:考虑由直线段(2个点)产生第一个图形(5个点)的过程。图1中,设1P 和5P 分别为原始直线段的两个端点,现需要在直线段的中间依次插入三个点2P ,3P ,4P 。显然2P 位于线段三分之一处,4P 位于线段三分之二处,3P 点的位置可看成是由4P 点以2P 点为轴心,逆时针旋转 600而得。旋转由正交矩阵)3cos()3sin()3sin()3cos(A实现。算法根据初始数据(1P 和5P 点的坐标),产生图1中5个结点的坐标。结点的坐标数组形成一个25矩阵,矩阵的第一行为1P 的坐标,第二行为2P 的坐标⋯⋯,第五行为5P 的坐标。矩阵的第一列元素分别为5个结点的 x 坐标,第二列元素分别为5个结点的 y 坐标。进一步考虑 Koch 曲线形成过程中结点数目的变化规律。设第k 次迭代产生的结点数为kn ,第1k次迭代产生的结点数为1kn,则kn 和1kn中间的递推关系为341kknn。三、实验程序及注释:p=[0 0;10 0]; %P为初始两个点的坐标, 第一列为 x坐标 , 第二列为 y坐标n=2; %n为结点数A=[cos(pi/3) -sin(pi/3);sin(pi/3) cos(pi/3)]; %旋转矩阵for k=1:4 d=diff(p)/3; %diff 计算相邻两个点的坐标之差, 得到相邻两点确定的向量%则d就计算出每个向量长度的三分之一, 与题中将线段三等分对应 m=4*n-3; %迭代公式 q=p(1:n-1,:); %以原点为起点, 前n-1 个点的坐标为终点形成向量 p(5:4:m,:)=p(2:n,:); %迭代后处于 4k+1 位置上的点的坐标为迭代前的相应坐标 p(2:4:m,:)=q+d; %用向量方法计算迭代后处于4k+2位置上的点的坐标 p(3:4:m,:)=q+d+d*A'; %用向量方法计算迭代后处于4k+3位置上的点的坐标 p(4:4:m,:)=q+2*d; %用向量方法计算迭代后处于4k位置上的点的坐标 n=m; %迭代后新的结点数目endplot(p(:,1),p(:,2)) %绘出每相邻两个点的连线axis([0 10 0 10]) 四、实验数据记录:由第三部分的程序,可得到如下的Koch分形曲线:图2 五、注记:1.参照实验方法,可绘制如下生成元的Koch 分形曲线:图3 此时,旋转...