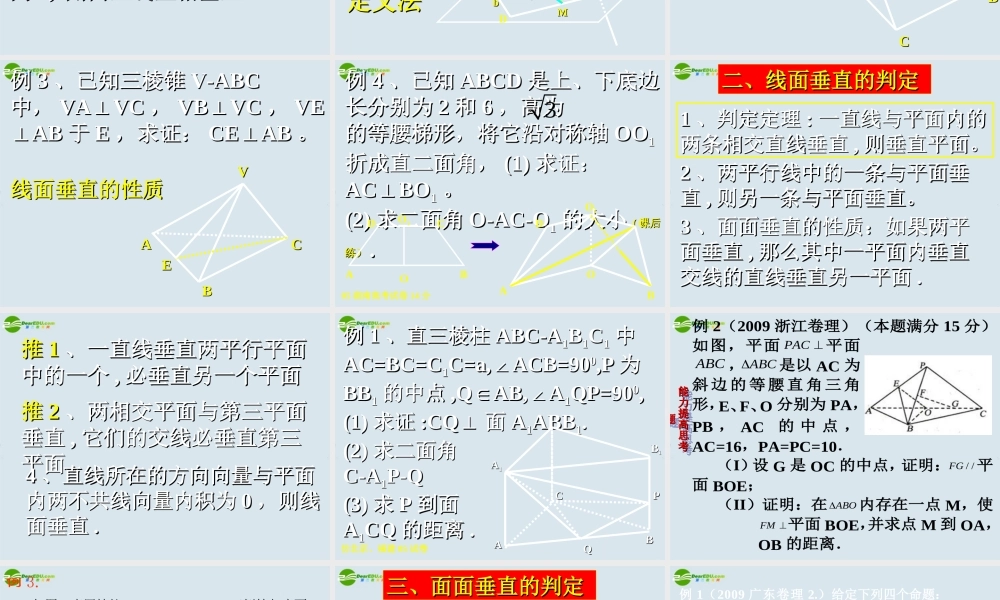
位置关系位置关系二、垂直问题的证明二、垂直问题的证明常见问题:常见问题:1 、直线与直线垂直的证明;2 、直线与平面垂直的证明;33 、平面与平面垂直的证明;、平面与平面垂直的证明;二、垂直问题的证明二、垂直问题的证明二、垂直问题的证明二、垂直问题的证明二、垂直问题的证明二、垂直问题的证明二、垂直问题的证明二、垂直问题的证明一、线线垂直的判定一、线线垂直的判定11 、定义:两条直线所成的角为、定义:两条直线所成的角为909000,, 则两直线垂直。则两直线垂直。22 、定理:直线垂直两条平行直、定理:直线垂直两条平行直线中的一条线中的一条 ,, 与另一条垂直。与另一条垂直。33 、三垂线定理及逆定理:垂射、三垂线定理及逆定理:垂射则垂斜则垂斜 ;; 垂斜则垂射垂斜则垂射 ..一、线线垂直的判定一、线线垂直的判定44 、线面垂直的性质、线面垂直的性质 :: 如果直线如果直线与平面垂直与平面垂直 ,, 那么直线与平面内那么直线与平面内的任意直线垂直。的任意直线垂直。55 、如果两直线所在的向量内积、如果两直线所在的向量内积为为 0, 0, 则两直线互相垂直则两直线互相垂直 ..例例 11 、已知、已知 aa 、、 bb 是异面直是异面直线,线, aa 上两点上两点 AA 、、 BB 的距离为的距离为 88,, bb 上两点上两点 CC 、、 DD 的距离为的距离为66 ,, ADAD 、、 BCBC 的中点分别为的中点分别为 MM、、 NN ,且,且 MN=5MN=5 ,求证:,求证: ab⊥ab⊥。。BCCDbbAAaaMMNNOO定义法定义法例例 22 、已知三棱锥、已知三棱锥 V-ABCV-ABC 中,侧中,侧面面 AVBAVB 垂直侧面垂直侧面 BVCBVC ,, VAVA 垂垂直底面直底面 ABCABC ,求证:,求证: ABBC⊥ABBC⊥。。VVAABBCCDD线面垂直的性质线面垂直的性质例例 33 、已知三棱锥、已知三棱锥 V-ABCV-ABC中,中, VAVC⊥VAVC⊥,, VBVC⊥VBVC⊥,, VEVEAB⊥AB⊥于于 EE ,求证:,求证: CEAB⊥CEAB⊥。。VVAABBEECC线面垂直的性质线面垂直的性质例例 44 、已知、已知 ABCDABCD 是上、下底边是上、下底边长分别为长分别为 22 和和 66 ,高为 ,高为 的等腰梯形,将它沿对称轴的等腰梯形,将它沿对称轴 OOOO11折成直二面角,折成直二面角, (1)(1) 求证:求证:ACBO⊥ACBO⊥11 。。(2)(2) 求二面角求二面角 O-AC-OO-AC-O11 的大小的大小 (( 课后课后练)练) ..3ABCDOO1ABODCO105 湖南高...